SOLUTION: Show that the side of a rectangle whose area is 100 meter^2 with minimum perimeter is 10 meter

Algebra ->  Geometry-proofs -> SOLUTION: Show that the side of a rectangle whose area is 100 meter^2 with minimum perimeter is 10 meter      Log On


   

Question 1148244: Show that the side of a rectangle whose area is 100 meter^2 with minimum perimeter is 10 meter
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.

They want you to prove that 

    if  x and y are two positive real numbers whose product is 100,  x*y = 100, 

    then the the minimum value of x+y is achieved at x = y = 10.

It is simple calculus problem.


Solution 

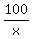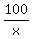If x*y = 100,  then  y = 100%2Fx,  and the sum  x+y  is  x + 100%2Fx.


This function of "x",  f(x) = x + 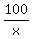100%2Fx  achieves the minimum when its derivative is equal to zero


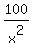    f'(x) = 1 - 100%2Fx%5E2 = 0.


Then   x%5E2 = 100;  hence  x = sqrt%28100%29 = 10.


Thus we proved that if  x*y = 100,  then  x+y has minimum at  x = y = 10.

Solved.