Question 1148217: Determine the numbers of solutions for each part then solve, if possible.
Triangle KLM: K=39 degrees, k=10cm , m=15.0cm
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! check out my diagrams.
they tell you the answer to your problem, which is 2 solutions.
check out the reference indicated as well.
it talks about the ambiguous case, which is the main theme that the problem is addressing.
here's the reference.
https://mathbitsnotebook.com/Geometry/TrigApps/TAUsingLawSines.html
here's the diagrams.

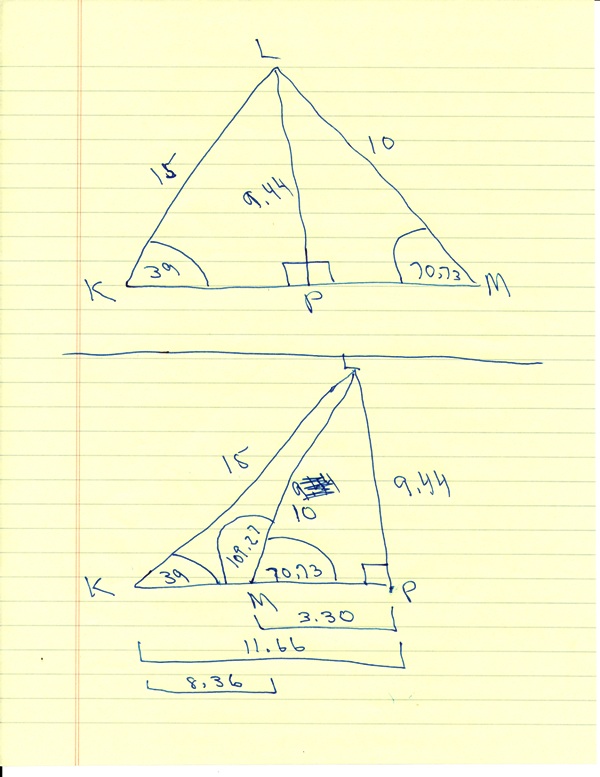
in the first diagram, the law of sines was used to find angle M.
the formula used was k/sin(K) = m/sin(M)
this formula was solved for M in the following manner:
sin(M) = m * sin(K) / k
this became sin(M) = 15 * sin(39) / 10
angle M was then found by taking arcsin(15 * sin(39) / 10)
that got you angle M = 70.73 degrees, rounded to 2 decimal places.
that led to angle L being 70.27 degrees because the sum of the angles of a triangle is 180 degrees.
in the second diagram, the supplement of angle M was found.
that supplement was 180 - angle (M).
that made the supplement to angle M equal to 109.27 degrees.
that led to angle L being 31.73 degrees because the sum of the angle of a triangle is 180 degrees.
the second diagram is a valid solution as well.
angle M could be 71.73 degrees or it could be 109.27 degrees.
that gave you 2 possible solutions to the problem.
in the third diagram, i used the first diagram and dropped a perpendicular from L to P.
i used trigonometry to find the length of LP.
the diagram showed that LM was lager than LP and smaller than LK.
that led to the fourth diagram, where LM was swung like a pendulum to the other side of LP.
triangle LMP in the second diagram was congruent to triangle LMP in the fourth diagram.
angle LMP remained the same.
angle LMK was supplement to angle LMP and therefore equal to 180 - 70.73 = 109.27 degrees.
i used trigonometry to find the length of MP, KP and KM.
the specific trigonometry was using the cosine function rather than the fine function.
in the fourth diagram:
cos(39) = KP / 15 led to KP = 15 * cos(39) making KP equal to 11.66.
cos(70.73 = MP / 10 led to MP = 10 * cos(70.73) making MP equal to 3.30.
KM = KP minus MP = 11.66 minus 3.20 making KM equal to 8.36.
note that KM was found using the law of sines in diagram 2 and also found using trigonometry in diagram 4.
all 4 diagrams contributed to the solution.
the solution is that there are two possible solutions to the problem.
the reference explains what is happening in pretty good detail as well, although the numbers in the reference are different because they are using a different example.
|
|
|