Question 1148051: Use the graphical method to solve the following question. Scale: 2 cm: 10 units on both axes.
A butcher produces sausage from a blend of beef, pork and fat. Batches of 50 kg of the mixture are made up. He must ensure that there is at most one quarter the amount of pork as there is beef. The fat is used as a filler and each 50 kg portion of sausage should not contain more than 10 kg of the latter to maintain the quality. The costs per kg of beef, pork and fat are N$6-00, N$4-00 and N$2-00 respectively. Determine how the 50 kg batches should be made up to minimize the costs and calculate the minimum cost.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! x = the number of kilograms of beef.
y = the number of kilograms of pork.
z = the number of kilograms of fat.
your constraint equations are:
x + y + z = 50
z <= 10
y <= .25 * x
x >= 0
y >= 0
your objective function is:
cost = 6 * x + 4 * y + 2 * z
if you are dealing with a two dimensional graph, then you have to find a way to reduce the number of variables to two instead of 3.
you can use some logic here.
since the cost of fat is the cheapest, it makes sense that you would want to maximize the use of fat.
that means that you would use 10 kilograms of fat in whatever mixture you need.
therefore, your objective function becomes cost =
6 * x + 4 * y + 20
a little logic in your constraint equations will allow you to eliminate z from those as well.
if z <= 10, that means the x + y >= 40.
you can replace z <= 10 with x + y >= 40.
your constraint equations become:
x + y = 40
x + y >= 40
y <= .25 * x
x >= 0
y >= 0
those top two constraint equations are conflicting, but you will get the same answer whether you use one or the other.
i'll do it all three ways to show you the answer becomes the same regardless of which way you choose to do it.
using the desmos.com calculator, you would graph the opposite of these constraints.
the area of the graph that is not shaded is your region of feasibility.
the corner points of that region are where your least cost solution lies.
first graph uses all the constraint inequality opposites.
you would graph.
x + y = 40]
x + y <= 40
x >= .25 * x
x <= 0
y <= 0
that graph looks like this:
second graph uses x + y <= 40 and not x + y = 40:
x + y <= 40
x >= .25 * x
x <= 0
y <= 0
third graph uses x + y = 40 and not x + y <= 40:
x + y = 40
x >= .25 * x
x <= 0
y <= 0
in the third graph, the solution has to be on the line x + y = 40.
don't forget that we are graphing the opposite of the inequalities and the region of feasibility becomes the area of the graph that is not shaded.
you will see that all graphs point to two possible solutions.
they are:
(x,y) = (32,8) or (x,y) = (40,0)
your objective function is cost = 6 * x + 4 * y + 20
at your two possible low cost points, the objective function is evaluated to get:
when x = 32 and y = 8, the cost is equal to 32 * 6 + 8 * 4 + 20 = 244
when x = 40 and y = 0, the cost is equal to 40 * 6 + 0 * 4 + 20 = 260.
you have a lowest cost solution when x = 32 and y = 8.
the lowest cost is equal to 244.
all constraint requirements are met, as they have to be.
x >= 0 becomes 32 >= 0 which is true.
y >= 0 becomes 8 >= 0 which is true.
y <= .25 * x becomes 8 <= .25 * 32 which becomes 8 <= 8 which is true.
i used a linear programming simplex tool to confirm this would be the least possible cost solution if we used all three variables.
the results from the linear programming simplex tool confirmed the solution is correct.
a picture of the results from that tool is shown below.
the linear equation simplex tool couldn't handle y <= .25x, so i had to change that inequality to y - .25x <= 0 by subtracting .25x from both sides of it.
i included x >= 0 and y >= 0, but the simplex tool didn't require that, so i could have left them out and gotten the same result.
the simplex tool confiirmed that the low cost solution is when x = 32 and y = 8.
that's your solution.
your lowest cost will be when you use 32 kilograms of beef and 8 kilograms of pork and 10 kilogramas of fat the mixture.
Answer by ikleyn(52784)  (Show Source):
You can put this solution on YOUR website! .
This problem can be solved VERY QUICKLY, by the very simple way and without using the Linear programming approach.
Let x = the amount of beef, in kilograms;
y = the amount of pork;
z = the amount of fat.
Your constraint equations are:
x + y + z = 50
z <= 10
y <= 0.25x
x >= 0, y >= 0
Your objective function to minimize is
cost = 6x + 4y + 2z
Since fat is cheapest ingredient, the butcher decides to use all 10 kg of fat.
Than your constraints take the form
x + y = 40 (1)
y <= 0.25x (2)
x >= 0, y >= 0 (3)
and your task now is to minimize the form
cost = 6x + 4y + 20
which is the same as to minimize
cost' = 6x + 4y. (4)
So, your problem is just reduced to 2 variables.
Next, from (1), express y = 40-x and substitute it into (4) and (2). You will get the function to minimize
cost' = 6x + 4*(40-x) = 160 + 2x (5)
under the restriction (2)
40-x <= 0.25x, or 40 <= x + 0.25x = 1.25x, which is x >= 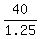 = 32. (6)
Formula (5) says "than lesser is x, than lesser is the value of the function c' = 160+2x."
But formula (6) says that you CAN NOT take x lesser than 32.
Thus, x= 32 kilograms of beef is the solution.
Then the full and complete ANSWER is
x= 32 kilograms of beef, y= 40-32 = 8 kilograms of pork and z= 10 kilograms of fat.
Solved (!)
Solved even without using Linear programming approach (!) (!)
Solved at the level accessible even for 6 - 7- 8 grade middle school students level (!) (!!) (!!!)
|
|
|
