Question 1147872: Solve the Absolute Value Inequality:
1a. Solve the inequality:|x−5|<6.
Based on the method described in your Essential Review, to rewite this as a compound inequality itwould look like:
The solution to the inequality in interval notation is:
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52893)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem asks you to find all values of "x", remoted less than 6 units from 5 in the number line.
The solution set is, OBVIOUSLY, -1 < x < 11, or, in the interval form, (-1,11).
Solved.
-----------------
It is the SHORTEST and MOST STRAIGHTFORWARD way solving this type of absolute value inequalities.
See the lesson
- Solving absolute value inequalities
in this site.
See also the list of accompanied lessons, listed at the end of this lesson.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Indeed the fastest and easiest way to solve an absolute value inequality like this is as tutor @ikleyn said: interpret

as meaning "the difference between x and 5 is less than 6".
That is easily interpreted on a number line. 5-6 = -1, so -1 is one number that is 6 away from 5; 5+6 = 11, so 11 is the other number that is 6 away from 5. Then since the inequality asks for all the numbers whose distance from 5 is LESS THAN 6, the answer is everything greater than -1 and less than 11.
But I suspect that solution method is not what is found in your "Essential Review". Most likely, the expected method is something like this:
 means means 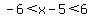 . To solve that compound inequality, add 5 to all three parts: . To solve that compound inequality, add 5 to all three parts:
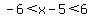
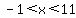
or, in interval notation as required, (-1,11).
Note that method of solution LOOKS easier than the other method. And for this basic problem involving inequalities, it probably is. But when the absolute value inequalities get more complicated, you will find it easier to use the other method.
So that other method is a good thing to learn to use...
|
|
|