SOLUTION: object A and B with the same mass m=2kg undergo a direct central impact. Before the impact, A is moving to the right with a velocity of 4m/s and B is stationary. Determine the velo

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: object A and B with the same mass m=2kg undergo a direct central impact. Before the impact, A is moving to the right with a velocity of 4m/s and B is stationary. Determine the velo      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1147662: object A and B with the same mass m=2kg undergo a direct central impact. Before the impact, A is moving to the right with a velocity of 4m/s and B is stationary. Determine the velocity of A after impact If the impact is perfectly plastic.
Answer by ikleyn(52847) About Me  (Show Source):
You can put this solution on YOUR website!
.

If the impact is "perfectly plastic", it means that after the collision, the two mass joint (clue) in one mass 2 + 2 = 4 kg.


This term also means that the momentum conservation law is held.


The mechanical energy conservation law is not held in this case: part of the mechanical energy transforms in the heat energy,

so the mechanical energy conservation  law IS NOT included to the model in this case.


Only the momentum conservation law works, and it is just enought.


So, your equation, based on the momentum conservation law, is


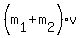    %28m%5B1%5D%2Bm%5B2%5D%29%2Av = 2*4 + 2*0.


The left side is the momentum after the collision;  the right side is the momentum before the collision.


The value of "v" in the left side is the resulting speed of the joint mass 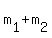 m%5B1%5D%2Bm%5B2%5D.


Substitute the values of masses into the last equation, simplfy and solve for "v", the only unknown.


    (2 + 2)*v = 2*4 + 2*0

     4v       =  8

      v       = 8/4 = 2 m/s.


ANSWER.  The velocity of the joint mass after the impact is 2 m/s.

Solved.

--------------

Notice that the question to the problem is formulated INCORRECTLY.

The correct formulation is  THIS : 

    "Determine the velocity of the  joint mass  after impact,  if the impact is perfectly plastic."

Also note,  that instead of the term  "the impact is perfectly plastic",  more often the term  "the impact is perfectly inelastic"  is used.