SOLUTION: A pair of dice are tossed twice. Find the probability that the first roll is a total of at least 6 and the second roll is a total of at least 9.

When a pair of dice are tossed once, the sample space is the set of 36 pairs (a,b) of integer numbers "a" and "b"

from 1 to 6 inclusively, with the probability    for each event (pair).



When a pair of dice are tossed twice, the sample space is the set of 36*36 pairs (a,b) and (x,y) of integer numbers "a", "b", x and y

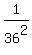from 1 to 6 inclusively, with the probability    for each event (which is two pairs {(a,b),(x,y)} ).


The probability that the first roll is a total of at least 6 is


    P( the total of the first tossing) >= 6) = P(6) + P(7) + P(8) + P(9) + P(10) + P(11) + P(12).


    P(6)  is 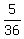      //   6 = 1+5 = 2+4 = 3+3 = 4+2 = 5+1

    P(7)  is       //   7 = 1+6 = 2+5 = 3+4 = 4+3 = 5+2 = 6+1

    P(8)  is 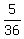      //   8 = 2+6 = 3+5 = 4+4 = 5+3 = 6+2

    P(9)  is 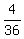      //   9 = 3+6 = 4+5 = 5+4 = 6+3

    P(10) is 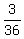      //  10 = 4+6 = 5+5 = 6+4

    P(11) is   

    P(12) is   


Therefore, P( the total of the first tossing) >= 6) =  =  = .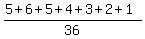




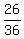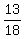The probability that the second roll is a total of at least 9 is


    P( the total of the second tossing) >= 9) = P(9) + P(10) + P(11) + P(12) =  =  = .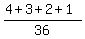

                

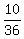The outcomes of the first and second rolls are INDEPENDENT, therefore, the final probability under the question is


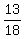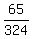    . = .    ANSWER