SOLUTION: A river boat takes 4 hours when going with the current from point A to point B (along a straight river), while its engine is using maximum power (the boat is at full speed). It tak

Let "d" be the distance between the points A and B along the river.


Let "u" be the motorboat speed in still water and let "v" be the speed of the current.



Then the effective speed of the motorboat with the current (downstream) is 

    u + v =      (1)


while the effective speed against the current (upstream) is 

    u - v = 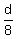.    (2)



Subtract equation (2) from equation (1).  You will get

       2v =  =  -  = .


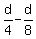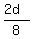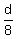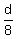Hence,  v = .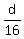


Thus the current speed is 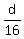   units of length per hour.


Now notice, that the motorboat with the engine turned off travels along the river with the effective speed, 
EQUAL to the speed of the current.


It means that the motorboat with the engine turned off will cover the distance "d" from A to B in


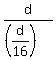     = 16 hours.


It is the ANSWER  to the problem's question:  16 hours.

    1)  the solution and the answer DO NOT DEPEND on units of length (!).


    2)  the solution and the answer are valid for any value of "d", the distance between the points (!) 


    3)  The idea of the solution is simple: first find the speed of the current in terms of "d";

        then take into account that the speed of the motorboat with the engine turned off is precisely equal

        to the speed of the current.