Question 1147433: How many more possible arrangements can be made using the letters of the word PERMUTATIONS than using the letters of the word COMBINATIONS?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Word "PERMUTATIONS" has 12 symbols, of them "T" has multiplicity 2, and the rest symbols have multiplicity 1.
Therefore, the number of distinguishable arrangements of the word "PERMUTATIONS" is
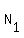 = =  = =  = 239500800. (1)
In the formula (1), 2! in the denominator serves to account for repeating "T" in the word.
Word "COMBINATIONS" has 12 symbols, of them
- the letter "O" has multiplicity 2,
- the letter "I" has multiplicity 2,
- and all other letters are not repeating.
Therefore, the number of distinguishable arrangements of the word "COMBINATIONS" is = 239500800. (1)
In the formula (1), 2! in the denominator serves to account for repeating "T" in the word.
Word "COMBINATIONS" has 12 symbols, of them
- the letter "O" has multiplicity 2,
- the letter "I" has multiplicity 2,
- and all other letters are not repeating.
Therefore, the number of distinguishable arrangements of the word "COMBINATIONS" is
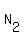 = = 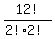 = = 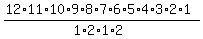 = 119750400. (2)
In the formula (2), two factors of 2! in the denominator serves to account for repeating letters "O" and "I" in the word.
The difference = 119750400. (2)
In the formula (2), two factors of 2! in the denominator serves to account for repeating letters "O" and "I" in the word.
The difference 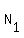 - - 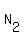 = 239500800 - 119750400 = 119750400. ANSWER = 239500800 - 119750400 = 119750400. ANSWER
Solved, completed and explained in all details.
------------------
On Permutations, see the lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
- Arranging elements of sets containing indistinguishable elements
- Persons sitting around a cicular table
- Combinatoric problems for entities other than permutations and combinations
- Miscellaneous problems on permutations, combinations and other combinatoric entities
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|