SOLUTION: The demand function for a product is p=128−8q where p is the price in dollars when q units are demanded. Find the level of production that maximizes the total revenue and

Revenue R is the product of values of  "q"  and "p"


    R = q*p = q*(128-8q).


In this form, it is a quadratic function of "q", presented as the product of two linear binomials.


The roots of R as the function of "q"  are  q = 0  and  q = 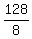 = 16.


The maximum value of R as the function of "q"  is exactly half way between the roots.


Thus you found that the maximum of R(q)  is achieved at  q= 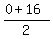 = 8.


The value of the maximum is  


    R(8) = 8*(128 - 8*8) = 8*(128-64) = 8*64 = 512.