SOLUTION: Solve for n n!/4!(n-2)! =3

Cancel (n-2)! in both the numerator and denominator.   You will get


     = 3,    or


     = 3.


It is equivalent to


    n*(n-1) = 3*24 = 72.     (1)


Now quickly guess the solution  n =  .      ANSWER


     // --- There was a typical "typo" in my original post, which I just fixed here. ---
     //     Thanks to tutors who noticed it (!)


Or, if you want to solve equation (1) algebraically, then please do it . . . 

Tutor @IKLEYN made a mistake. n ACTUALLY = 9.

**Duly noted, Edwin. Thanks!

I agree with you, 100%. I didn't even notice it but you're correct. The way it's written indicates:  but as you stated and as we saw it,

the denominator should be clearly stated, by using an open parenthesis where the denominator begins, as follows: n1/(4!(n - 1)!) = 3, which would render as: 

Thanks again for pointing this out, Edwin! 

I'll say this mainly for Ikleyn's benefit.  Yours too if you're tuned in
MathTherapy.  Students almost never have to write algebra all on one line
anymore, EXCEPT ON THIS SITE! and most of them do not understand Igor's "formula
notation" program, which I use extensively. Thus I forgive them for a certain
implication of the order of operations never having dawned upon them, for I'm
sure that their teachers have never brought it up to them. That is, if a
numerator or denominator contains more than one term, or has more than one
factor showing, then the entire numerator or denominator must go inside
parentheses.  Incidentally, even Igor's "formula notation" contains a
flaw, for it falsely assumes

a/bc, typed with three "{"'s before it and three "}"'s after it, means this



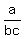when it actually means this: 

 

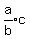I wrote Igor about this years ago, but he seemed to think I was wrong, and 
never fixed it.  I didn't want to have an argument, so I've just lived with it.  

Anyway I always assume parentheses around a numerator or denominator were meant
when it would change the meaning to something more likely to be what the student
meant.  So I assume this problem should be:

n!/(4!(n-2)!) = 3

and I forgive this student for not putting parentheses around the denominator he
meant:

I am pretty sure this student meant this:



Thus,









Multiply both sides by the denominator on the left:











We disregard the negative answer, since factorials are
only defined for non-negative integers. So,

answer = 9 is correct.

Edwin