Question 1147251: A series of 10584 consecutive integers has a sum that is a perfect cube. What is the smallest possible average of this series?
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sum of a series of consecutive integers is the number of integers, multiplied by the average of the integers.
The sum of a series of 10584 consecutive integers is 10584 times the average of the integers.
Note that the average of an odd number of consecutive integers is an integer, and the average of an even number of consecutive integers is halfway between two integers. So the average we are looking for is halfway between two integers.
The prime factorization of 10584 is
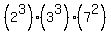
So problem is asking us to find the smallest possible average k/2 for which k is an odd integer and the sum
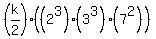
is a perfect cube.
That is not possible. If k is an odd integer, then the prime factorization of that expression will contain 2^2, which makes it impossible for the sum to be a perfect cube.
ANSWER: The problem as stated has no solution.
Note the difficulty with the problem as stated is that the average of an even number of consecutive integers is halfway between two integers, and the product
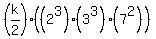
can never be a perfect cube.
If we change the problem by doubling the number of consecutive integers, then we can find a solution.
Then we have 21168 consecutive integers; the prime factorization of 21168 is
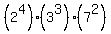
and we need the product
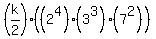
to be a perfect cube.
And now k=7 works; the average of the 21168 consecutive integers is 7/2.
To check that answer, we find the series has 10584 integers either side of 7/2 = 3.5, making the series from -10580 to +10587. In the sum, the negatives and positives cancel, leaving us with a sum of 10581+10582+...+10587 = 74088, which is 42^3.
|
|
|