Question 1147211: Sherlock made an elaborate code to remember the 10-digit combination to his locker. This is the code he came up with:
A - K - B - J - C - H - D - G - E - F
Each letter stands for a different single digit number, from 0-9.
To find the combination, study the clues below to figure out what digit is represented by each letter. When two letters are written together without an operation symbol, they represent a tens digit and a ones digit.
D + D + D = F
H + H = B
G + B +E = F + A +C
J + A = CC
F x D = KG (x means multiplied by)
B / H = K (/ means divided by)
D x H = CK
A x H = KE
J / D = K
D H (this is fractions, D over J and H over B)
- = -
J B
What is the 10 digit combination to Sherlock's locker?
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 , so , so 
Then  , so , so 
Hence  . .
We therefore also have a bunch of doubling pairs: 1-2, 2-4, 3-6, 4-8. But  , so , so 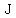 and and  are either 3-6 or 4-8. are either 3-6 or 4-8.
Note that 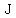 & &  are one set, and are one set, and 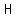 & &  are the other distinct set. are the other distinct set.
Further,  and and  are a are a 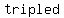 pair. pair.
Note that  , so , so = 1,2,3. But from above, = 1,2,3. But from above,  =3,4, so =3,4, so  . .
Then  and and  . Further, . Further, 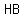 must be the other double pair available, 4-8. Hence must be the other double pair available, 4-8. Hence  and and  . .
Now,  , so , so  . .
Since  and and  , , 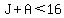 so so  and and  . .
Further,  . Then . Then  => =>  , so , so  . .
solution: 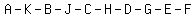 is is 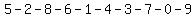
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given:
1. D + D + D = F
2. H + H = B
3. G + B +E = F + A +C
4, J + A = CC
5. F x D = KG
6. B / H = K
7. D x H = CK
8. A x H = KE
9. J / D = K
10. D/J = H/B
Analysis…
From 4, C is 1
From all the given information together, E and G are the only possible letters for 0.
If G is 0, then 5 tells us either D or F is 5; but 1 tells us neither D nor F can be 5.
So G is not 0; therefore E is 0.
Since E is 0, 8 tells us either A or H is 5.
But 10 tells us H can’t be 5.
So A is 5.
Then 4 tells us J is 6.
Then, since J is 6, 9 tells us D and K are, in some order, 2 and 3.
But D can’t be 2, because 1 would make F 6, but J is 6.
So D is 3; and so K is 2.
Then 1 tells us F is 9.
Then 5 tells us G is 7.
8 tells us H is 4.
6 tells us B is 8.
His code is
A - K - B - J - C - H - D - G - E - F = 5286143709
|
|
|