SOLUTION: Among employees of a certain firm, 70% know C/C++, 60% know Java, and 90% know at least one of the two languages. (a) What is the probability that a selected programmer knows bot

First of all, let me notice, that your questions (a), (b) and (c) are posed INCORRECTLY.

My EDITING to your questions is as follows.



    (a) What is the probability that a selected  employee knows both languages?
    (b) What is the probability that a selected  employee knows C/C++ but not Java?
    (c) What is the probability that a selected  employee knows only one of the two languages?


     The rest of questions (d), (e) and (f) are correct.

We are given  

    P(C) = 0.7,  P(J) = 0.6,  and  P(C U J) = 0.9.


Then   P(C ∩ J) = P(C) + P(J) - P(C U J) = 0.7 + 0.6 - 0.9 = 0.4.



       Now I am in position to answer all questions, one after another.



(a)  This probability is  P(C ∩ J) = 0.4.



(b)  This set is  C \ (C ∩ J);  therefore,

     this probability is equal to  P(C) - P(C ∩ J) = 0.7 - 0.4 = 0.3.



(c)  This probability is equal to  P(C U J) - P(C ∩ J) = 0.9 - 0.4 = 0.5.



(d)  This probability is  P(C ∩ J)/P(J) =  = .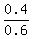



(e)  This probability is  P(C ∩ J)/P(C) =  = .



(f)  To answer first part, compare  P(C)*P(J) with P(C ∩ J).

          They are different;  therefore, the answer is  "NO".


     To answer the second part,  compare  P(C ∩ J) with 0 (zero, ZERO).

          They are different;  therefore, the answer is  "NO".