Question 1147027: Hi
A B and C had 181 cookies at first. A gave away 20% of her cookies while B bought 28 more cookies. C also bought more cookies and had 4 times as many as before. Then the ratio of the number of cookies A B C had was 2:5:8 respectively. How many cookies did B have at first.
thanks
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52795)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let "a", "b" and "c" be the numbers of cookies that A, B and C had originally.
The first equation is
a + b + c = 181. (1)
After all events, A had 0.8a cookies, B had (b+28) and C had 4c cookies.
We are given this long proportion 0.8a : (b+28) : 4c = 2 : 5 : 8.
It means that
0.8a = 2x,
b+28 = 5x
4c = 8x
for some unknown number x.
From these equations,
a = 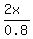 , (2)
b = 5x - 28 (3)
c = 2x. (4)
Substitute it into equation (1). You will get , (2)
b = 5x - 28 (3)
c = 2x. (4)
Substitute it into equation (1). You will get
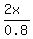 + (5x-28) + 2x = 181.
Now solve this equation and find "x".
Then find "a", "b" and "c" from (2), (3) and (4).
Check if your answer are INTEGER numbers. + (5x-28) + 2x = 181.
Now solve this equation and find "x".
Then find "a", "b" and "c" from (2), (3) and (4).
Check if your answer are INTEGER numbers.
Just instructed / and completed.
|
|
|