Question 1146878: In a right triangle, the length of one of the legs is 8 cm and the measure of the acute angle opposite to this leg is 50°. Find the measure of the other acute angle and the lengths of the other leg and the hypotenuse.
Found 4 solutions by josmiceli, ikleyn, Theo, MathTherapy:
Answer by josmiceli(19441)   (Show Source):
Answer by ikleyn(52814)  (Show Source):
You can put this solution on YOUR website! .
In a right triangle, the length of one of the legs is 8 cm and the measure of the acute angle opposite to this leg is 50°.
Find the measure of the other acute angle and the lengths of the other leg and the hypotenuse.
~~~~~~~~~~~~~~~~~~
The other acute angle is 90° - 50° = 40°.
The other leg is 8*tan(40°).
The hypotenuse is  .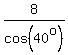
When I see the solutions of some tutors at this forum that use INADEQUATELY complicated tools for simple tasks,
I often doubt if they know the Math, at all.
When you work with right triangles, the "law of sine theorem" is irrelevant ---- the trigonometric functions perform all needed operations . . .
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! you can use the law of sines to solve this.
law of sines says a/sin(A) = b/sin(B) = c/sin(C)
let your triangle be ABC
A is the 90 degree angle.
B is the 40 degree angle.
C is the 50 degree angle.
a is the side opposite angle (A)
b is the side opposite angle (B)
c is the side opposite angle (C)
measure of side c is 8.
measure of angle (C) is 50 degrees.
since angle A is 90 degrees, then angle B has to be 180 - 90 - 50 = 40 degrees.
law of sines says a/sin(A) = c/sin(C)
c = 8 and C = 50 and A = 90
formula becomes:
a/sin(90) = 8/sin(50)
solve for a to get:
a = 8 * sin(90) / sin(50) = 10.44325831
likewise, .....
c/sin(C) = b/sin(B)
this becomes:
8/sin(50) = b/sin(40)
solve for b to get:
b = 8 * sin(40) / sin(50) = 6.712797049
this is a right triangle where:
the two legs are c and b, and he hypotenuse is a.
your leg measurements are:
c = 8
b = 6.712797049
the hypotenuse measurement is:
c = 10.44325831
in a right triangle, the sum of the square of each leg is equal to the square of the hypotenuse.
that means that 6.712797049^2 + 8^2 = 10.44325831^2
do the math and you will see that 109.0616442 = 109.0616442, confirming that the lengths of the legs and the hypotenuse are correct.
your solution is:
the other acute angle is 40 degrees.
the length of the other leg is 6.712797049
the length of the hypotenuse is 10.44325831
here's my diagram.
Answer by MathTherapy(10555)  (Show Source):
|
|
|
