SOLUTION: A newspaper carrier has $4.35 in change. He has six more quarters than dimes but two times as many nickels as quarters. How many coins of each type does he have?

Click here to see ALL problems on Word Problems With Coins

Question 1146739: A newspaper carrier has $4.35 in change. He has six more quarters than dimes but two times as many nickels as quarters. How many coins of each type does he have?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website!

SUBSTITUTE:
----------solve this for q.

Answer by ikleyn(52897)   (Show Source):
You can put this solution on YOUR website!
.

            This problem is to be solved using one single equation in one unknown.

            I will show you on how to do it.

            The major step is to choose the leading unknown reasonably.

Let x be the number of quarters. Then the number of dimes is (x-6), and the number of nickels is 2x. By knowing it, you can write the "money" equation momentarily 5*(2x) + 10*(x-6) + 25x = 435 cents. Simplify 10x + 10x - 60 + 25x = 435 45x = 435 + 60 = 495 x = 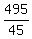= 11. ANSWER. 11 quarters; 11-6 = 5 dimes, and 2*11 = 22 nickels. CHECK. 5*22 + 5*10 + 25*11 = 435 cents, which is precisely correct (!)

Solved.

------------------

The lesson to learn from my post is THIS :

This problem can be solved using one single equation in one unknown. It is designed and intended to be solved in this way. It is intended for 6-7 grade students who are not familiar yet with systems of equations.

To see many other similar solved problems, look into the lessons
    - More complicated coin problems
in this site.

SOLUTION: A newspaper carrier has ​$4.35 in change. He has six more quarters than dimes but two times as many nickels as quarters. How many coins of each type does he​ have?

SOLUTION: A newspaper carrier has $4.35 in change. He has six more quarters than dimes but two times as many nickels as quarters. How many coins of each type does he have?