|
Question 1146601: Find the distance from point A(15,−21) to the line 5x+2y = 4. Round your answer to the nearest tenth.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the distance from point  to the given line to the given line
A( , ,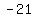 ), ),
 .....first, write in slope intercept form .....first, write in slope intercept form


The slope of your GIVEN line is  . .
The slope of the line you want to find (perpendicular line) must have slope inverse reciprocal which is  . .
Line you want:
 , using point-slope form , using point-slope form


WHY? The two lines intersect at some point which you will find.
Then use Distance formula to find the length from the intersection point to point A( , ,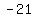 ). ).
You are first looking for the line perpendicular to the given one which contains point  . .
Now find intersection point of  and and  . So, all you need is equal right sides. . So, all you need is equal right sides.






go to  , plug in , plug in  and solve for and solve for 




intersection point is at ( , ,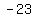 ) )
now use Distance formula to find the length from the intersection point to point A
A( , ,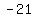 ) = ( ) = ( , , ) )
( , ,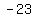 ) = ( ) = ( , , ) )





 => exact solution => exact solution
 =>to the nearest tenth =>to the nearest tenth
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor shows a detailed solution to the problem.
You should be able to understand all the steps required for the solution; and you should be able to solve a similar problem by that method.
However, in practice, there is a concise formula for finding the (shortest) distance from a given point to a given line. When the equation of the line is in the form Ax+By+C=0, then the distance from a point (p,q) to the line is

In the required form, the equation in this problem is 5x+2y-4 = 0. Then the distance from (15,-21) to that line is

|
|
|
| |