SOLUTION: Find the equations of the lines passing through the origin that are tangent to a circle with radius 2 and center at point (2, 1).

Algebra ->  Trigonometry-basics -> SOLUTION: Find the equations of the lines passing through the origin that are tangent to a circle with radius 2 and center at point (2, 1).      Log On


   

Question 1146382: Find the equations of the lines passing through the origin that are tangent to a circle with radius 2 and center at point (2, 1).
Answer by greenestamps(13214) About Me  (Show Source):
You can put this solution on YOUR website!


Clearly with a center (2,1) and radius 2, one of the two lines tangent to the circle passing through the origin is x=0.

Some work is needed to find the other line....

Let (a,b) be the other point of tangency to the given circle of a line that passes through the origin. Then

(1) The distance from (2,1) to (a,b) is 2:

%28b-1%29%5E2%2B%28a-2%29%5E2+=+2%5E2
b%5E2-2b%2B1%2Ba%5E2-4a%2B4+=+4
a%5E2%2Bb%5E2-4a-2b+=+-1

(2) The slope of the radius to the point of tangency is 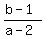%28b-1%29%2F%28a-2%29
The slope of the tangent line is the negative reciprocal, 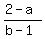%282-a%29%2F%28b-1%29
The tangent passes through the points (0,0) and (a,b); so an equation of the tangent is
b+=+%28%282-a%29%2F%28b-1%29%29a
b%28b-1%29+=+a%282-a%29
b%5E2-b+=+2a-a%5E2
a%5E2%2Bb%5E2-2a-b+=+0

Subtracting the equation in (1) from the equation in (2),

2a%2Bb+=+1
b+=+1-2a

Substituting b=1-2a in (2)...

%281-2a%29%28-2a%29+=+2a-a%5E2
-2a%2B4a%5E2+=+2a-a%5E2
5a%5E2-4a+=+0
a%285a-4%29+=+0
a+=+4%2F5

And then, to find b

b+=+1-2a+=+-3%2F5

The point (a,b) is (4/5,-3/5).

Since the tangent line passes through the origin, the equation of the line is y+=+%28-3%2F4%29x

A graph showing part of the lower half of the given circle and the second tangent line; the first tangent line is of course x=0, the y-axis:

graph%28400%2C400%2C-1%2C3%2C-2%2C2%2C-sqrt%284-%28x-2%29%5E2%29%2B1%2C%28-3%2F4%29x%29