Question 1145870: An auditorium has 550 balcony seats and 1800 main- level seats. If tickets for balcony seats will cost 20 dollars less than tickets for main- level seats, what should the prices be for each type of ticket so that the total revenue from a sellout performance will be 97,100?
Answer by ikleyn(52872)   (Show Source):
You can put this solution on YOUR website! .
Let x be price for a main-level seat (in dollars, of source).
The the price for the balcony seat is (x-20) dollars, according to the condition.
The equation for the revenue is
1800*x + 550*(x-20) = 97100 dollars.
From the equation, express x and calculate
x = 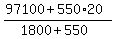 = 46 dollars.
ANSWER. 46 dollars for each main-level seat and 46-20 = 26 dollars for each balcony seat.
CHECK. 46*1800 + 26*550 = 97100 dollars. ! Precisely correct !
-----------------
Is everything clear to you in my solution ?
If not, let me know by posting through the "Thank you" window (which is for students' comments).
In this case, please refer to the problem's ID number, which is 1145870.
If you do not refer to this number, I will not know to whom to answer.
/\/\/\/\/\/\/\/
It is a standard tickets problem.
There are different methods of solving such problems.
Read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
From these lessons, learn on how to solve such problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
