Question 1145868: Anita's, a fast-food chain specializing in hot dogs and garlic fries, keeps track of the proportion of its customers who decide to eat in the restaurant (as opposed to ordering the food "to go"), so it can make decisions regarding the possible construction of in-store play areas, the attendance of its mascot Sammy at the franchise locations, and so on. Anita's reports that
45% of its customers order their food to go. If this proportion is correct, what is the probability that, in a random sample of 4 customers at Anita's, exactly 2 order their food to go?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is on Binomial distribution.
Use the Binomial Probability formula
Probability (P) (k successes in n trials) = nCk * p^k * (1-p)^(n-k), where nCk = n! / (k! * (n-k)!)
For this problem, n = 4, k = 2, p = 45% = 0.45.
Therefore,
P = 4C2 * (0.45)^2 * (1-0.45)^(4-2) = 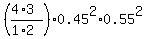 = 0.3675 = 36.75% = 0.3675 = 36.75%
Solved.
|
|
|