SOLUTION: A model rocket is launched with an initial an initial upward velocity of 50 m/s. The rockets height “h” (in meters) after “t” seconds is given by the following. H=50t-5t

Algebra ->  Rate-of-work-word-problems -> SOLUTION: A model rocket is launched with an initial an initial upward velocity of 50 m/s. The rockets height “h” (in meters) after “t” seconds is given by the following. H=50t-5t       Log On


   

Question 1145783: A model rocket is launched with an initial an initial upward velocity of 50 m/s. The rockets height “h” (in meters) after “t” seconds is given by the following.
H=50t-5t squared
Find all values of “t” for which the rockets height is 20 meters
Round your answer to the nearest hundredth
This was my answer? I just want to make sure it’s right!
Answer:3.25, 3.94
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
A model rocket is launched with an initial an initial upward velocity of 50 m/s. The rockets height “h” (in meters) after “t” seconds is given by the following.
H=50t-5t squared
Find all values of “t” for which the rockets height is 20 meters
-------
H=50t-5t^2 = 20
t^2 - 10t + 4 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-10x%2B4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10%29%5E2-4%2A1%2A4=84.

Discriminant d=84 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--10%2B-sqrt%28+84+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-10%29%2Bsqrt%28+84+%29%29%2F2%5C1+=+9.58257569495584
x%5B2%5D+=+%28-%28-10%29-sqrt%28+84+%29%29%2F2%5C1+=+0.41742430504416

Quadratic expression 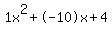1x%5E2%2B-10x%2B4 can be factored:
1x%5E2%2B-10x%2B4+=+%28x-9.58257569495584%29%2A%28x-0.41742430504416%29
Again, the answer is: 9.58257569495584, 0.41742430504416. Here's your graph:
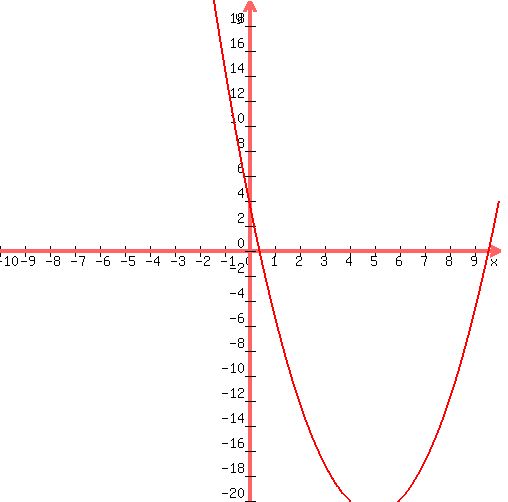graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-10%2Ax%2B4+%29

==================
This is more descriptive:
-5t^2 + 50t - 20 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -5x%5E2%2B50x%2B-20+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2850%29%5E2-4%2A-5%2A-20=2100.

Discriminant d=2100 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-50%2B-sqrt%28+2100+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2850%29%2Bsqrt%28+2100+%29%29%2F2%5C-5+=+0.41742430504416
x%5B2%5D+=+%28-%2850%29-sqrt%28+2100+%29%29%2F2%5C-5+=+9.58257569495584

Quadratic expression 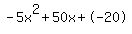-5x%5E2%2B50x%2B-20 can be factored:
-5x%5E2%2B50x%2B-20+=+%28x-0.41742430504416%29%2A%28x-9.58257569495584%29
Again, the answer is: 0.41742430504416, 9.58257569495584. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-5%2Ax%5E2%2B50%2Ax%2B-20+%29

=========================================================
Round your answer to the nearest hundredth
This was my answer? I just want to make sure it’s right!
Answer:3.25, 3.94
-------------------
It might be instructive to see how you got your answers.