Question 1145746: A brand name has a 40% recognition rate. Assume the owner of the brand wants to verify that rate by beginning with a small sample of 5 randomly selected consumers. Complete parts (a) through (d) below.
a. What is the probability that exactly 4 of the selected consumers recognize the brand name?
The probability that exactly 4 of the 5 consumers recognize the brand name is
0.131.
(Round to three decimal places as needed.)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
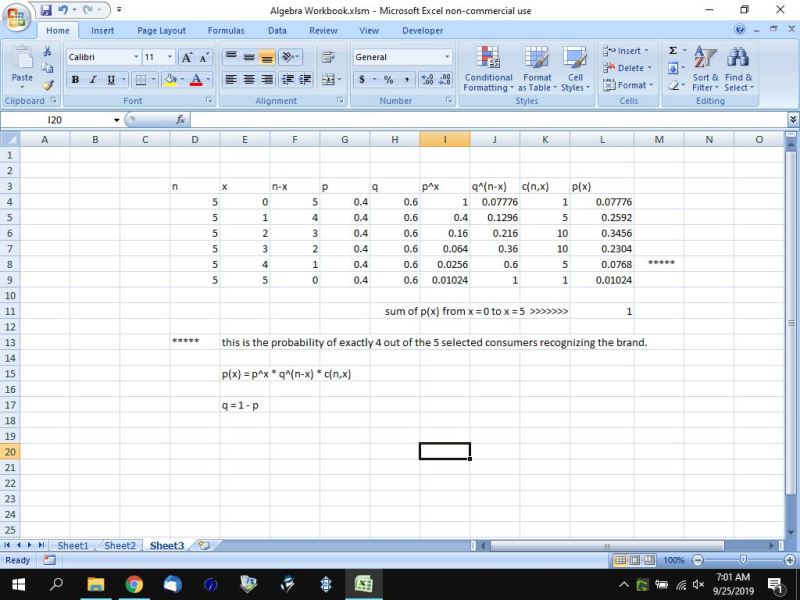
You can put this solution on YOUR website! p(4) = .4^4 * .6^1 * c(5,4) = .0768 = .077
this is a binomial distribution type problem where p(x) = p^x * q^(n-x) * c(n,x)
n is equal to 5
x ranges from 0 to 5.
c(n,x) = n! / (x! * (n-x)!)
the following excel spreadsheet shows all the probabilities from x = 0 to x = 5.
the sum of all the probabilities is equal to 1, as it should be.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I think that the modern trend in solving such problems is USING some effective TECHNOLOGY.
In my post, I will show you one robust technology.
With it, you will be able make calculations and solve similar problems in seconds.
This is a binomial distribution type problem where p(x) = C(n,x)* p^x * q^(n-x)
n is equal to 5 // number of trials
x is equal to 4 // number of success trials
p is the probability of success trial
q = 1 - p
C(n,x) = n! / (x! * (n-x)!) // binomial coefficient
In your case p(4) = C(5,4) * 0.4^4 * 0.6^1 = use Excel function BINOM.DIST(4, 5, 0.4, FALSE) = 0.0768. ANSWER
On Excel function BINOM.DIST, see its description everywhere, for example
https://support.office.com/en-us/article/binom-dist-function-c5ae37b6-f39c-4be2-94c2-509a1480770c
|
|
|