Question 1145696: The third term of an arithmetic sequence is -1 and the seventh term is -13; how would I find the explicit formula for this sequence, and what would a22 be?
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In the arithmetic sequence (or arithmetic progression) 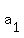 , ,  , , ,... ,...
each 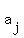 is related to the previous is related to the previous 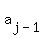 by a common difference, d. by a common difference, d.
This means we can write the progression as:
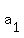 , , 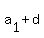 , , 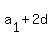 , ..., , ...,  , ... , ...
You are given 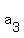 = -1 and = -1 and 


Subtracting the  expression from the expression from the  expression: expression:
 --> d = -3 --> d = -3
With the common difference, you can easily find  and then write and then write
 for n = 1,2,3,... for n = 1,2,3,...
If you plug in n=22 you will find 
---
EDITed to fix the display of the arithmetic progression (commas inside curly braces seem to break things).
Answer by ikleyn(52863)   (Show Source): (Show Source):
|
|
|