Question 1145689: Listed below are the amounts of time (in months) that the employees of a restaurant have been working at the restaurant. Find the standard deviation of the data set, rounding to one more decimal place than is present in the data.
2 3 5 13 22 35 60 86 101 122
Found 2 solutions by VFBundy, ikleyn:
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Calculate the mean of the set = 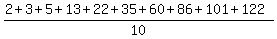 = 44.9 = 44.9
Subtract the mean from each data point:
2 - 44.9 = -42.9
3 - 44.9 = -41.9
5 - 44.9 = -39.9
13 - 44.9 = -31.9
22 - 44.9 = -22.9
35 - 44.9 = -9.9
60 - 44.9 = 15.1
86 - 44.9 = 41.1
101 - 44.9 = 56.1
122 - 44.9 = 77.1
Square each result:
(-42.9)² = 1840.41
(-41.9)² = 1755.61
(-39.9)² = 1592.01
(-31.9)² = 1017.61
(-22.9)² = 524.41
(-9.9)² = 98.01
(15.1)² = 228.01
(41.1)² = 1689.21
(56.1)² = 3147.21
(77.1)² = 5944.41
Find the sum of the squared values:
1840.41 + 1755.61 + 1592.01 + 1017.61 + 524.41 + 98.01 + 228.01 + 1689.21 + 3147.21 + 5944.41 = 17839.90
Because the data set is the entire population, divide the sum of the squared values by the number of data in the set*:
17839.90/10 = 1783.990
*(NOTE: If the data set were from a sample, and not the entire population, you would have divided by the number of data in the set minus 1.)
This is your variance: 1783.990. To find the standard deviation, take the square root of the variance...which is 42.2.
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If you insert the keywords "standard deviation online calculator" into the Google search engine,
you will get tens / (tons) web-sites, containing such calculators (free of charge (!) ) with detailed explanations
on what to do and how to use them.
So, you simply copy and past your line of numbers into the calculator input window and then press the "Calculate" button.
You will get the answer in seconds.
See, for example, this online calculator, which is the first in my list
https://www.calculator.net/standard-deviation-calculator.html
Another similar online calculator is in this site
https://www.algebra.com/algebra/homework/Probability-and-statistics/sample-standard-deviation.solver
This my post is not a hidden promotion of neither site . . .
|
|
|