SOLUTION: Suppose you want to fill nine 1-lb tins with a snack mix. You have $15 and plan to buy almonds for $2.45 per lb, hazelnuts for $1.85 per lb, and raisins for $.80 per lb. You want t

Algebra ->  Matrices-and-determiminant -> SOLUTION: Suppose you want to fill nine 1-lb tins with a snack mix. You have $15 and plan to buy almonds for $2.45 per lb, hazelnuts for $1.85 per lb, and raisins for $.80 per lb. You want t      Log On


   

Question 1145595: Suppose you want to fill nine 1-lb tins with a snack mix. You have $15 and plan to buy almonds for $2.45 per lb, hazelnuts for $1.85 per lb, and raisins for $.80 per lb. You want the mix to contain twice as much lf the nuts as the raisins by weight. How much of each ingredient should you buy?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
Nine pounds of the mixture needed 
NUTorRAISIN       PRICE per pound      QUANTITY     COST
Almonds            2.45                  a          2.45a
Hazelnuts          1.85                  h          1.85h
Raisins            0.80                  r          0.8r
TOTAL                                    9            15

system%28a%2Bh%2Br=9%2C2.45a%2B1.85h%2B0.8r=15%2Ca%2Bh=2r%29
Simplify and solve.

Notice E[1] and E[3] equations.
a%2Bh%2Br=9
2r%2Br=9
3r=9
r=3-----------three pounds for the raisins.

system%28a%2Bh=6%2C2.45a%2B1.85h%2B2.4=15%29
Simplify and solve for a and h from here...

Finished Solution:
system%28a=2%261%2F2%2Ch=3%261%2F2%2Cr=3%29

Answer by ikleyn(52812) About Me  (Show Source):
You can put this solution on YOUR website!
.
Suppose you want to fill nine 1-lb tins with a snack mix. You have $15 and plan to buy almonds for $2.45 per lb,
hazelnuts for $1.85 per lb, and raisins for $.80 per lb. You want the mix to contain twice as much
highlight%28cross%28lf%29%29 lb the nuts as the raisins by weight. How much of each ingredient should you buy?
~~~~~~~~~~~~~~~


            From the first glance,  this problem is for  3  equations in three unknowns.

            But actually,  it can be easily solved using only  ONE  single equation in  ONE  unknown.

            I will show you how to do it.


Solution 

Let  x be the amount of raisins by weight, in pounds.

Then the amount of the nuts is 2x pounds, according to the condition.

And the amount of almonds is then the rest (9-x-2x) = 9-3x.


The total cost equation is then


    0.80*x + 1.85*(2x) + 2.45*(9-3x) = 15.00    dollars.


Simplify and solve for x :


    0.80x + 3.70x + 2.45*9 - 7.35x = 15.00,

      x  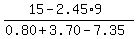                    = %2815.00-2.45%2A9%29%2F%280.80+%2B+3.70+-+7.35%29 = 2.47 pounds of raisins.


ANSWER.  2.47 pounds of raisins;  2*2.47 = 4.94 pounds of nuts, and the rest (9 - 3*2.47) = 1.59 pounds of almonds.

-----------------

The benefit of this approach is that students may start solving such problems much earlier than they start learning systems of equations.

I think that the true goal of this problem is to teach students to this approach.

=================

If you do not like these ugly number in the answer, then double check your input (!)

=================

To see other similar solved problems, look into the lessons
    - More complicated word problems to solve using a single linear equation
    - Advanced word problems to solve using a single linear equation
in this site.


/\/\/\/\/\/\/\/\

Be aware ! :   the setup in the post by  @josgarithmetic is  INCORRECT !