|
Question 1145593: You manage a clothing store and budget $6000 to restock 200 shirts. You can buy T-shirts for $12 each, polo shirts for $24 each, and rugby shirts for $36 each. If you want to have twice as many rugby shirts as polo shirts, how many of each type of shirt should you buy?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!
Let
t = # of t-shirts, cost $12 each
p = # of polo shirts, cost $24 each
r = # of rugby shirts, cost $36 each
You manage a clothing store and budget $6000 to restock 200 shirts.
(1) t+p+r = 200
(2) 12t+24p+36r = 6000
If you want to have twice as many rugby shirts as polo shirts...
(3) r = 2p
Substitute (3) into (1) and (2) to get two equations in t and p.
Then solve that pair of equations by your favorite method.
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
From the first glance, this problem is for 3 equations in three unknowns.
But actually, it can be easily solved using only ONE single equation in ONE unknown.
I will show you how to do it.
Solution
Let x be the number of polo shirts.
Then the number of rugby shirts is 2x, according to the condition.
And the number of T-shirts is then (200-x-2x) = 200-3x.
The total cost equation is then
24*x + 36*(2x) + 12*(200-3x) = 6000.
Simplify and solve for x :
24x + 72x + 12*200 - 36x = 6000,
60x = 6000 - 12*200
x = 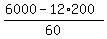 = 60.
ANSWER. 60 polo shirts; 60*2 = 120 rugby shirts and the rest, (200-60-2*60) = 20 are T-shirts.
-----------------
The benefit of this approach is that students may start solving such problems much earlier than they start learning systems of equations.
I think that the true goal of this problem is to teach students to this approach.
=================
To see other similar solved problems, look into the lessons
- More complicated word problems to solve using a single linear equation
- Advanced word problems to solve using a single linear equation
in this site.
|
|
|
| |
