.
1. ALGEBRA solution
Let x be the rate of work of the first tank, in "job per minute", which is "the tank volume per minute".
Then the rate of work of the second tank is 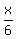 "the tank volume per minute".
In one minute, two pumps fill
"the tank volume per minute".
In one minute, two pumps fill  of the tank volume.
It means that
x +
of the tank volume.
It means that
x + 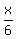 =
=  .
Multiply both sides of this equation by 216. You will get
216x + 36x = 1,
252x = 1
x =
.
Multiply both sides of this equation by 216. You will get
216x + 36x = 1,
252x = 1
x = 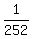 .
Hence, the first pump will fill the tank in 252 minutes, working alone. ANSWER
.
Hence, the first pump will fill the tank in 252 minutes, working alone. ANSWER
2. Mental solution (logical reasoning)
The first, faster pump works as productively, as 6 slower pumps.
So, the given info, if reformulated, says that 6+1 = 7 slower pumps will fill the tank in 216 minutes.
Hence, one slower pump will do it in 7*216 minutes.
The faster tank will do it 6 times faster, i.e. in 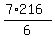 = 7*36 = 252 minutes.
You got the same answer as above.
= 7*36 = 252 minutes.
You got the same answer as above.
My congrats (!)
Now you know TWO METHODS to solve the problem.
------------------
It is a standard and typical joint work problem.
There is a wide variety of similar solved joint-work problems with detailed explanations in this site. See the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.