Question 1145271: IF THE CHOLESTEROL LEVEL OF MEN IN THE COMMUNITY IS NORMALLY DISTRIBUTED WITH A MEAN OF 200 AND SD OF 25 WHAT IS THE PROBABILITY THAT A RANDOMLY SELECTED SAMPLE OF 49 MEN WILL HAVE A MEAN BETWEEN 190 AND 250.
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, you want to find the standard deviation of the sample. You do this by taking the standard deviation of the population and dividing it by the square root of the number of men in the sample:
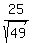 = 25/7 = 3.57 = 25/7 = 3.57
To find the probability that men have a cholesterol level below 250, subtract the mean from 250, then divide this result by the standard deviation of the sample:
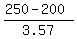 = 50/3.57 = 14.00 = 50/3.57 = 14.00
This is the z-score. Normally, you would go to a z-table and look for this value. But, when you go to a z-table, a value of 14.00 is off the charts. For all intents and purposes, the score is 1, meaning there is a 100% probability that men have a cholesterol level below 250.
To find the probability that men have a cholesterol level below 190, subtract the mean from 250, then divide this result by the standard deviation of the sample:
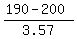 = -10/3.57 = -2.80 = -10/3.57 = -2.80
This is the z-score. Go to a z-table and look for this value. You will find that the result is 0.0026. This means there is a 0.0026 probability that men have a cholesterol level below 190.
To find the probability that men have cholesterol scores between 190 and 250, subtract the probability that men have a cholesterol level below 190 (0.0026) from the probability that men have a cholesterol level below 250 (1) to get a result of 0.9974.
|
|
|