|
Question 114525: Find the center, vertices and foci of the ellipse. Graph the ellipse. would someone please explain this process fully, I've been somewhat confused and this question will be on the final exam.
(X^2/4)+(y^2/9) = 1
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Fortunately, your equation is in standard form for an ellipse, namely:
An ellipse with a semimajor axis a and semiminor axis b, centered at the point (h,k) and having its major axis parallel to the y-axis may be specified by the equation:  . .
So, for your equation  , the values are: , the values are:
h = 0
k = 0
a = 3
b = 2
So we know that the center of the ellipse is at the origin, (0, 0) and the major axis is the y-axis because the y term has the larger denominator.
The vertices are the points on the ellipse that intersect the major axis. Since the major axis is on the y-axis, we know that the x coordinates of the vertices are 0. All we need do is solve the equation for two values of y when the value of x is 0 to determine the y-coordinates of the vertices.



 or or  . .
Hence, the vertices are at (0,3) and (0,-3)
In order to locate the foci (one focus, two foci), we need to calculate another parameter called the eccentricity  . The eccentricity of an ellipse tells us how round or how stretched out it is. . The eccentricity of an ellipse tells us how round or how stretched out it is. 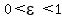
If  then you have a circle, then you have a circle,  must be less than 1 otherwise you won't have an ellipse any longer, it would be a straight line. must be less than 1 otherwise you won't have an ellipse any longer, it would be a straight line.
Since we know the semi-major and semi-minor axis lengths a and b, we can calculate  . In this case . In this case 
Now we need one more relationship involving the eccentricity.  where c is the distance from the center to either focus. In our case, we need to calculate c, so where c is the distance from the center to either focus. In our case, we need to calculate c, so 
We know that the foci lie on the major axis, so again the x-coordinates of the points we seek will be 0. And the y-coordinates can be obtained by adding and subtracting our new found value of c to/from the y-coordinate of the center.
Therefore the foci are at ( , ,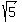 ) and ( ) and ( , , ) )
Word of warning: If you get the EXACT same problem on your final, no worries. But be careful! Look closely at the denominators in the original equation. The term with the largest denominator will determine whether it is a vertical ellipse, like this one, or a horizontal ellipse. If the x term has the big denominator, you will have to turn things around so that the x term denominator is 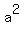 and do your calculations based on the fact that the major axis is parallel (or coincident with) to the x-axis. It might help to remember that a is always larger than b in the general equation. and do your calculations based on the fact that the major axis is parallel (or coincident with) to the x-axis. It might help to remember that a is always larger than b in the general equation.
|
|
|
| |