Question 1145144: 4.The median life of Brand LT5 batteries is 100 hours. What is the probability that in a set of three such batteries, at least two will last longer than 100 hours?
Answer by ikleyn(52851)   (Show Source):
You can put this solution on YOUR website! .
From the first glance, it is clear that the given info/input is NOT SUFFICIENT to solve the problem - so, appropriate
auxiliary assumptions should be made.
Moreover, making appropriate and likelihood assumptions is the PART of the solution.
Having nothing else given, an appropriate hypothesis is to assume that we have continuous random variable
X = "the time of a Brand LT5 battery service / (or "life")"
with random values that are uniformly distributed with the minimum value of 0 and the maximum value of 200 hours.
Then the mean average is exactly 100, as the problem states, and the condition becomes "consistent with the given part" and "self-closed".
Then the probability P(X < 100) =  , as well as P(x > 100) = .
Therefore, the probability that at least two of the three batteries will last longer than 100 hours is  +  =  +  =  = .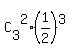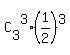
Solved.
-------------------
To see many other similar solved problems, look into the lesson
- Unusual probability problems
in this site.
In particular, this problem is VERY SIMILAR to the solved Problem 4 of that lesson.
|
|
|
