Question 1145140: If the polynomial p(x) = (x^5 - 6x + 7)^2019 - (x^5 - 6x + 9)^2020 + 5x^5 - 30x + 50 is divided by x^5 - 6x + 8,
Then, find the remainder.
Answer by ikleyn(52876)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First addend,  , gives the remainder (-1)^2019 = -1, when divided by x^5 - 6x + 8. OBVIOUSLY.
Second addend, , gives the remainder (-1)^2019 = -1, when divided by x^5 - 6x + 8. OBVIOUSLY.
Second addend, 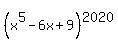 , gives the remainder 1^2020 = 1, when divided by x^5 - 6x + 8. OBVIOUSLY.
Third addend, , gives the remainder 1^2020 = 1, when divided by x^5 - 6x + 8. OBVIOUSLY.
Third addend, 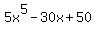 , gives the remainder 42, when divided by x^5 - 6x + 8. OBVIOUSLY.
Thus we know all three partial remainders, and are in position to answer the question now.
ANSWER. The remainder under the question is -1 - 1 + 42 = 40. , gives the remainder 42, when divided by x^5 - 6x + 8. OBVIOUSLY.
Thus we know all three partial remainders, and are in position to answer the question now.
ANSWER. The remainder under the question is -1 - 1 + 42 = 40.
Solved, answered, explained and completed.
---------------
Nice problem (!) An Olympiad level (!)
Thanks for posting it : it was a pleasure to me to solve it (!)
Come again soon to this forum to learn something new (!)
|
|
|