Question 1145119: Richard has just been given a 6-question multiple-choice quiz in his history class. Each question has four answers, of which only one is correct. Since Richard has not attended class recently, he doesn't know any of the answers. Assuming that Richard guesses on all six questions, find the indicated probabilities. (Round your answers to three decimal places.)
(a) What is the probability that he will answer all questions correctly?
(b) What is the probability that he will answer all questions incorrectly?
(c) What is the probability that he will answer at least one of the questions correctly? Compute this probability two ways. First, use the rule for mutually exclusive events and the probabilities shown in the binomial probability distribution table.
Then use the fact that P(r ≥ 1) = 1 − P(r = 0).
Compare the two results. Should they be equal? Are they equal? If not, how do you account for the difference?
They should be equal, but may not be due to table error.
They should not be equal, but are equal.
They should be equal, but may differ slightly due to rounding error.
They should be equal, but differ substantially.
(d) What is the probability that Richard will answer at least half the questions correctly?
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) Having 4 optional answers to each question, of which only one is correct,
the probability to guess the answer correctly is  , if to guess randomly.
Therefore, the probability to guess all 6 answers correctly is , if to guess randomly.
Therefore, the probability to guess all 6 answers correctly is 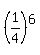 = = 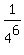 = 0.000244. ANSWER
(b) Since the probability to guess answer correctly is = 0.000244. ANSWER
(b) Since the probability to guess answer correctly is  to each question,
the probability to answer incorrectly is to each question,
the probability to answer incorrectly is  for each question.
Therefore, the probability to guess all 6 answers incorrectly is for each question.
Therefore, the probability to guess all 6 answers incorrectly is 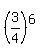 = 0.177979. ANSWER
(c) Before answering the last question (c), I'd like to notice that the post INCORRECTLY uses the notion / (the conception)
of mutually exclusive events, showing that the author of the post doesn't know the terminology in the subject.
The correct term to use here is "complementary probability".
After making this notice, I am ready to continue.
The probability to answer at least one question correctly is the COMPLEMENT to the probability to answer all questions incorrectly,
i.e. the complement to the probability found in (b).
Thus the answer to (c) is 1 - = 0.177979. ANSWER
(c) Before answering the last question (c), I'd like to notice that the post INCORRECTLY uses the notion / (the conception)
of mutually exclusive events, showing that the author of the post doesn't know the terminology in the subject.
The correct term to use here is "complementary probability".
After making this notice, I am ready to continue.
The probability to answer at least one question correctly is the COMPLEMENT to the probability to answer all questions incorrectly,
i.e. the complement to the probability found in (b).
Thus the answer to (c) is 1 - 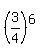 = 1 - 0.177979 = 0.822021. ANSWER = 1 - 0.177979 = 0.822021. ANSWER
Solved and completed.
I do not go to the remaining part of the post, since it is more similar to writing essay than to Math.
--------------------
For introductory lessons on Probability, see
- Simple and simplest probability problems
- Solving probability problems using complementary probability
- Elementary Probability problems related to combinations
- A True/False test
- A multiple choice answers test
- A shipment containing fair and defective alarm clocks
- A drawer contains a mixture of socks
- Probability for a computer to be damaged by viruses
- Conditional probability problems
- Typical probability problems from the archive
- Experimental probability problems
- OVERVIEW of lessons on Probability
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|