SOLUTION: Solve by integration {{{dx/dt = t(x - 2)}}}

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Solve by integration {{{dx/dt = t(x - 2)}}}      Log On


   

Question 1145007: Solve by integration dx%2Fdt+=+t%28x+-+2%29
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
dx%2Fdt+=+t%28x+-+2%29

Multiply both sides by dt:

dx+=+t%28x+-+2%29%2Adt

The term on the right side contains two variables, t and x. We must get rid
of the other variable besides the variable of the differential.  The variable
of the differential on the right side is t (because we have dt), so we must
get rid of the (x - 2) factor.  So we divide both sides by (x - 2):

dx%2F%28x-2%29+=+%28t%28x+-+2%29%2Adt%29%2F%28x-2%29

dx%2F%28x-2%29+=+%28t%28cross%28x+-+2%29%29%2Adt%29%2F%28cross%28x-2%29%29

dx%2F%28x-2%29+=+t%2Adt%29

We integrate both sides:

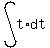int%28dx%2F%28x-2%29%29%22%22=%22%22int%28t%5E%22%22%2Adt%29%29

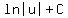We use the formula int%28du%2Fu%29%22%22=%22%22%22ln%7Cu%7C%22%2BC on the left side,
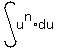
and we use the formula int%28u%5En%2Adu%29%22%22=%22%22u%5E%28n%2B1%29%2F%28n%2B1%29%2BC on the right side:

ln%28abs%28x-2%29%29=t%5E2%2F2%5E%22%22%2BC%5B1%5D

matrix%282%2C1%2C%22%22%2Ce%5E%28t%5E2%2BC%5B1%5D%29=abs%28x-2%29%29


Since the left side is positive, we can dispense with the absolute value on the
right side and require that x>2.

matrix%282%2C1%2C%22%22%2Ce%5E%28t%5E2%2BC%5B1%5D%29=x-2%29

matrix%282%2C1%2C%22%22%2Ce%5Et%5E2%2Ae%5EC%5B1%5D=x-2%29

Since eC1 is an arbitrary constant, we can let it be C.

matrix%282%2C1%2C%22%22%2CCe%5Et%5E2=x-2%29

matrix%282%2C1%2C%22%22%2Cx=Ce%5Et%5E2%2B2%29

Edwin