SOLUTION: Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probabil

Open your textbook or, even better, Wikipedia, the free encyclopedia at this page

https://en.wikipedia.org/wiki/Binomial_distribution


and read the following.


    In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution 
    of the number of successes in a sequence of n independent experiments, each asking a yes  -  no question, and each 
    with its own boolean-valued outcome: success/yes/true/one (with probability p) or failure/no/false/zero (with probability q = 1 − p). 


    The probability of getting exactly k successes in n trials is given by the probability mass function:

        Pr(k;n,p) = 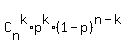   for k = 0, 1, 2, ..., n, where

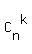        = n!/(k!(n-k)!)


It is impossible to explain this subject better than Wikipedia does it, in the short and coinciding form.