SOLUTION: The speed of a moving walkway is about 4.4 feet per second. Walking on the moving​ walkway, it takes Fred a total of 50 seconds to travel 110 feet with the movement of the walkwa

Let x be Fred's normal walking speed, in feet per second (the value under the question.


Then   Fred' speed moving with walkway is  (x+ 4.4) ft/s, 

while  Fred' speed moving with against walkway is  (x- 4.4) ft/s.


The time moving 110 ft with walkway is 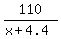 seconds,

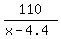while the time moving 110 ft against walkway is  seconds.


The total two-ways time moving forward and back is 


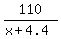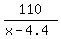     +  = 50  seconds.


It is your time equation.  All its terms are time periods.


To solve it, multiply both sides by  (x-4.4)*(x+4.4) = 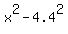 = .  You will get then


    110*(x + 4.4) + 110*(x - 4.4) = 50*(x^2 - 19.36).

    220x                = 50x^2 - 968

    50x^2 - 220x - 968 = 0

      =  = .


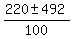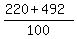Only positive root  x =  is meaningful, which gives you the


ANSWER.  Fred's normal walking speed is about 7.12 ft/s, according to the given data.


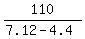CHECK.   +  = 50 seconds (approximately).


My comment.  My solution and my answer are correct - it was CHECKED.

             But the answer of 7.12 ft/s does not seem to be likelihood,

             which means that the input data in the post are not realistic.