.
Q(x) = 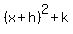 =
= 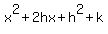 .
The fact that this polynomial gives the remainder 16, when it is divided by x, means that
h^2 + k = 16. (1)
Then the polynomial takes the form
Q(x) =
.
The fact that this polynomial gives the remainder 16, when it is divided by x, means that
h^2 + k = 16. (1)
Then the polynomial takes the form
Q(x) = 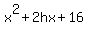 . (2)
Next, we are given that (x+2) divides this polynomial.
It means that x= -2 is its root (the Remainder Theorem).
Write this equation Q(-2) = 0. Due to (2), it takes the form
((-2)^2 + 2h*(-2) + 16 = 0.
Simplify and find "h" :
4 - 4h + 16 = 0,
4h = 16 + 4
4h = 20
h =
. (2)
Next, we are given that (x+2) divides this polynomial.
It means that x= -2 is its root (the Remainder Theorem).
Write this equation Q(-2) = 0. Due to (2), it takes the form
((-2)^2 + 2h*(-2) + 16 = 0.
Simplify and find "h" :
4 - 4h + 16 = 0,
4h = 16 + 4
4h = 20
h =  = 5.
Now substitute this value h= 5 into formula (1). You will get
5^2 + k = 16,
25 + k = 16,
k = 16 - 25 = -9.
ANSWER. h= 5; k= = -9.
= 5.
Now substitute this value h= 5 into formula (1). You will get
5^2 + k = 16,
25 + k = 16,
k = 16 - 25 = -9.
ANSWER. h= 5; k= = -9.
Solved.