SOLUTION: Given that the area of a rhombus is 40cm² and that each side has a length of 15cm, find the angles of the Rhombus

Algebra ->  Surface-area -> SOLUTION: Given that the area of a rhombus is 40cm² and that each side has a length of 15cm, find the angles of the Rhombus       Log On


   

Question 1144413: Given that the area of a rhombus is 40cm² and that each side has a length of 15cm, find the angles of the Rhombus
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.
For each parallelogram, its area is the product of the lengths of any two its adjacent sides

by the sine of the angle between them


    Area = 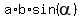a%2Ab%2Asin%28alpha%29.


For a rhombus, this formula takes the form


    Area = a%5E2%2Asin%28alpha%29,


where "a" is the length of any side and alpha is any of the four angles of the rhombus.


Thus in our case


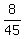    40 = 15%5E2%2Asin%28alpha%29,   sin%28alpha%29 = 40%2F225 = 8%2F45,


and an acute angle of the rhombus is


    alpha = arcsin%288%2F45%29 = arcsin(0.17778) = 0.17873 radians = 10.25 degrees (approximately).    ANSWER

Solved.

----------------

See the lesson
    - Area of a parallelogram
in this site.