SOLUTION: Susan makes and sells necklaces on a beach. When she sells the necklaces for Php 100 each, she sells an average of 20 necklaces per day. When she increases the price to Php 120, th

(A)  When the price is Php 100 for necklace, she sells 120 necklaces.

     When the price is Php 120  for necklace, she sells 120-2 necklaces.


    The demand function  d(p) is the function, which says how many necklaces (d) is sold at a given price (p).


    So, in your case, the demand function takes the value of 120 (necklaces)  at the price of Php 100 and

    decreases by 2 when the price increases by Php 20.


    Since the function is assumed to be linear, it means that  d(p) = 120 - 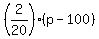, or, equivalently,  d(p) = 120 - 0.1*(p-100).


    It is the ANSWER to question (A).


    CHECK it :  if p= 100, you have d(100) = 120 - 0.1*(100-100) = 120 - 0.1*0 = 120.                                 ! Precisely Correct !

                if p= 120, you have d(120) = 120 - 0.1*(120-100) = 120 - 0.1*20 = 120-2 = 118.    ! Drop by 2, which is PRECISELY Correct !



(B)  Question (B) is even easier (!)


     The revenue function is the product of the price for single unit to the number of units.

      In your case, the revenue function is the product of the price "p" by the number of units "d(p)", which represent the number of units.


      So, you have  R(p) = p*d(p) = p*(120 - 0.1*(p-100)).


      You just have the revenue function R(p) as the function of price "p", expressed in this way.


      You can simplify it:
 

          R(p) = 120p - 0.1*p^2 + 10p = -0.1*p^2 + 130p.


      It is your final ANSWER to question (B).


      Notice, that the demand function d(p) is a linear function of the argument "p".

                   The revenue function R(p) is a quadratic function of price "p".