Question 1144267: The length of a rectangle is 2 feet more than the width. The area of the rectangle is 2 square feet. What are the dimensions of the rectangle?
Found 3 solutions by Alan3354, Theo, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! l = length
w = width
l = w + 2
area = l * w, and since l = w + 2, then area = (w + 2) * w = w^2 + 2w.
since area = 2, then 2 = w^2 + 2w.
subtract 2 from both sides of the equation to get w^2 + 2w - 2 = 0
factor this quadratic equation to get:
w = .7320508076 or w = -2.7320508076
w has to be positive so w = .7320508076
since area = length * width, and since area = 2 and since width = .7320508076 and since length = width + 2, then length = 2.7320508076.
length * width = .7320508076 * 2.7320508076 = 2
this confirms the solution is correct.
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For this problem, I will show you two ways (two methods) of solution.
First way is TRADITIONAL. You may find it everywhere, and it is boring.
If x is the width, then the length is (x+2) and the area equation is
x*(x+2) = 2 square feet,
x^2 + 2x - 2 = 0.
Use the quadratic formula
 = = 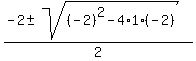 = = 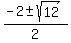 = = 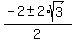 = = 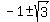 .
The width should be positive, so only positive root x = .
The width should be positive, so only positive root x = 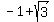 is the solution for the width.
ANSWER. The width is W = is the solution for the width.
ANSWER. The width is W =  . The length is L = W+2 = . The length is L = W+2 = 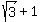 . .
The other method is fresh as a matutinal dawn in May, unexpected and elegant.
You may learn it only from me at this forum and in this site -- and practically nowhere else.
Let "x" be an unknown value on number line exactly half-way between the length L and the width W values of the rectangle.
Then, OBVIOUSLY, x = W + 1 = L - 1, and the area is
L*W = (x+1)*(x-1) = 2, or
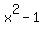 = 2, i.e. = 2, i.e.
 = 2 + 1 = 3;
hence, x = = 2 + 1 = 3;
hence, x =  .
Thus the dimensions of the rectangle are W = x-1 = .
Thus the dimensions of the rectangle are W = x-1 =  (the width) and L = x+1 = (the width) and L = x+1 = 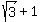 (the length).
You got the same answer, in a quick and simple manner. (the length).
You got the same answer, in a quick and simple manner.
See the lessons
- HOW TO solve the problem on quadratic equation mentally and avoid boring calculations
- Problems on the area and the dimensions of a rectangle
- Three methods to find the dimensions of a rectangle when its perimeter and the area are given
- Three methods to find the dimensions of a rectangle when its area and the difference of two dimensions are given
in this site,
where you will find many other similar solved problems (your TEMPLATES) with detailed explanations.
--------------
Come again soon to this forum to learn more (!)
|
|
|