SOLUTION: Can someone help me with this? Thank you. I need to find all the zeros of the function f(x)=-2x^4-5x^3-5x^2-20x+12, given -3 is a zero.

You can apply the "Rational roots theorem" first.


The theorem will tell you that possible rational roots are among some finite set of rational and integer numbers. 


It is good, but does not help too much.


Therefore, in such cases I simply make a plot of the polynomial, and the plot (see the Figure below) points you 
all possible real / rational / integer roots.


    


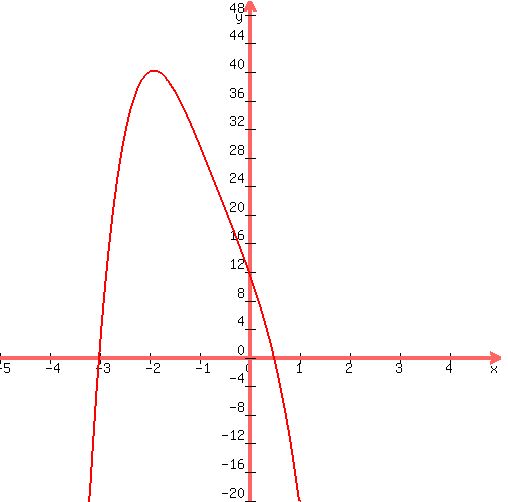    Plot y = 


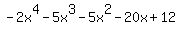In this case the roots -3 and  are pointed.


Surely, having this tip, you should check directly that these numbers really are the roots.


But if it is so, then the polynomial is divisible by the binomials  (x-(-3)) = (x+3)  and  (2x-1).


Thus the polynomial should be divisible by the product  (x+3)*(2x-1) = 2x^2 + 5x - 6 without a remainder.


So, make this long division and find the quotient. The quotient will be the polynomial of the degree 2 (quadratic).


Finding the roots of this quadratic is elementary job. (The rest of the roots could be complex numbers, though).


In this way, you will get the answer.