SOLUTION: one side of a parallelogram is 10m and its diagonal are 16m and 24m, respectively. Find its area.

The area of a parallelogram is the base times the height.  We are given the
base as 10m, so we only need the height.  We know that the diagonals of a
parallelogram bisect each other, So the two sides of the triangle are half
the diagonals 16m and 24m, so the two slanted sides of the triangle are
8m and 12m.

We use the law of cosines to calculate angle q.





Now we extend the base and draw in the height h:



Now we have the green right triangle in which:

The OPPOSITE side of theta is height h, and the HYPOTENUSE is the longer given
diagonal, which is 24m.  So



Put a 1 under the sine:



Cross-multiply:





Edwin 

For any parallelogram, the diagonals divide it in four triangles, whose areas are equal (!)


It is useful to know this fact, and it is easy to deduce it.


Indeed, let    and    be the lengths of the two diagonals and   be the angle between the diagonals.


Then the area of each of four triangles is  A = 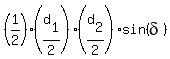.     (1)



Diagonals bisect each other and 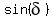   is the same for all 4 small triangles,

which proves the statement.



The area of each of four triangles can be calculated using the Heron's formula

    A = ,

where " s " is semi-perimeter and a, b, and c are the sides of small triangles.



In our case,  a= 10, b= 8 and c= 12,  so s =  =  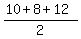=  = 15,  and the area of each small triangle is

    A =  =  =  =  = .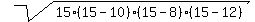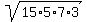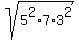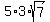


The full area of the parallelogram is 4 times it, i.e. 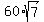  = 158.7451  (approximately; correct with 3 decimal places).