C(n+1,r) = C(n,r-1) + C(n,r)
which is often written this way:
 We'll use the facts that
We'll use the facts that
 ,
,  and
and  We'll prove the right side equals the left side:
We'll prove the right side equals the left side:
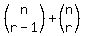
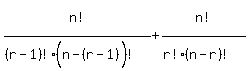

 Rewrite (n-r+1)! in the left denominator and r! in the right denominator:
Rewrite (n-r+1)! in the left denominator and r! in the right denominator:
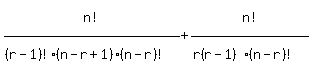 The LCD is r(r-1)!(n-r+1)(n-r)!
The LCD is r(r-1)!(n-r+1)(n-r)!
 Factor n! out of the numerator and rewrite the denominator:
Factor n! out of the numerator and rewrite the denominator:


 Rewrite the numerator as (n+1)! and the (n-r+1)! as (n+1-r)!
Rewrite the numerator as (n+1)! and the (n-r+1)! as (n+1-r)!
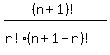 That's the same as the original left side:
That's the same as the original left side:
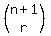 Edwin
Edwin