Question 1143846: At first, Josh and May had some marbles each. After Josh gave 1/4 of his marbles to May. May had 3 times as many marbles as him. May then gave Josh 12 marbles. In the end, each of them had an equal number of marbles. How many marbles did May have at first? Please help
Found 3 solutions by greenestamps, KMST, ikleyn:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll help you get started; you should have the experience of doing the work to get the answer yourself.
In the beginning, Josh has j marbles and May has m marbles:
Josh = j;
May = m
Then Josh gives 1/4 of his marbles to May:
Josh = j-(1/4)j = (3/4)j;
May = m+(1/4)j
At this point, May has 3 times as many marbles as Josh:
(1) 
Next May gives 12 marbles to Josh:
Josh = (3/4)j+12;
May = m+(1/4)j-12
Now the two have the same number of marbles:
(2) 
There you have 2 equations in j and m; use whatever method you like for solving pairs of equations to solve the problem.
While there are many ways to do that, the path I followed was to solve equation (1) for m and substitute that value in (2).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE ALGEBRA CLASS SOLUTION:
We have two unknown numbers, so we need two variables.
We are given two facts, so we can make two equations.
Choosing variables is an art, but practice makes you a better artist.
My variables:
Josh starts with 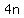 marbles (n is a positive integer), and marbles (n is a positive integer), and  is the number of marbles Josh gives May. is the number of marbles Josh gives May.
May starts with  marbles. marbles.
Fist Fact: "After Josh gave 1/4 of his marbles to May,
May had 3 times as many marbles as him."
My first equation draft:  . .
(I can simplify that equation to  ). ).
Second Fact: "May then gave Josh 12 marbles.
In the end, each of them had an equal number of marbles."
My second equation draft:  . .
(I can simplify that equation to  ). ).
At that point, I solve fornr  first, first,
substituting 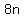 for for  in my second equation. in my second equation.
Then, I use the  value found to find value found to find  using the first equation. using the first equation.
THE FIFTH GRADER SOLUTION:
The fifth grader uses trial and error, tabulating results of each try.
Josh starts with a number of marbles that is a multiple of 4.
There are three points in the story:
the start, when Josh has 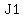 marbles and May has marbles and May has 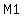 , ,
the midpoint, when they have 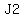 and and 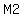 marbles, marbles,
and the end, when they have 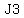 and and 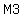 marbles. marbles.
It could be  , or 8, or 12, or 16, and so on. , or 8, or 12, or 16, and so on.
That would be the first numbered entered on the table.
After he gives 1/4 of his marbles to May, Josh has 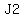 marbles, marbles,
and May has 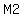 marbles, and those are the next entries. marbles, and those are the next entries.
The fifth grader does not worry about 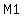 , ,
because he realizes try #1 did not work.
He just keeps calculating until he gets to both kids having
the same number  of marbles at the end. of marbles at the end.
Here is the fifth grader's table:

Looking at the line that end in "24 24" ,
the fifth grader realizes that
if May had  marbles after receiving marbles after receiving  marbles from Josh, marbles from Josh,
she must have started with  . .
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
After seeing the solutions from two our respectful tutors, you, probably, have a wish to see something more simple.
I will try to satisfy this desire by presenting as simple solution as possible.
From the condition, it is clear that the number of marbles Josh had initially, is multiple of 4.
Let x be 1/4 of Josh's marbles, that he had initially.
So, Josh had initially 4x marbles; at the first exchange, he gave 1/4 of it, i.e. x marbles, to May.
Thus after first exchange, Josh left with 3x marbles, while May had 3 times 3x marbles, i.e. 9x marbles.
After the second exchange, Josh has (3x+12) marbles, while May has (9x-12) marbles.
These amounts are the same, so you have this simple equation
3x + 12 = 9x - 12.
You can EASILY solve it :
12 + 12 = 9x - 3x, or 24 = 6x, which implies x= 24/6 = 4.
Thus Josh had initially 4x = 16 marbles.
After first exchange, May had 9x = 9*4 = 36 marbles; but 4 of them came from Josh (! remember, x= 4 !),
so May had initially 36 - 4 = 32 marbles. ANSWER
Solved.
|
|
|