SOLUTION: what the slope of the tangent line of the curve x^2-xy+y^2=3 at a point (1,2)

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: what the slope of the tangent line of the curve x^2-xy+y^2=3 at a point (1,2)      Log On


   

Question 1143793: what the slope of the tangent line of the curve x^2-xy+y^2=3 at a point (1,2)
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.

To answer the question, find the derivative y' = %28dy%29%2F%28dx%29.

For it, differentiate the given equation. You will get


    2x - y - xy' + 2y*y' = 0,


which implies


    2x - y = xy' - 2y*y',    or

    2x - y = y'*(x - 2y)

    y' = %282x-y%29%2F%28x-2y%29.


Now substitute the coordinates of the given point  x= 1, y= 2  into the last formula to get


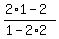    y' = %282%2A1-2%29%2F%281+-+2%2A2%29 = 0.


ANSWER.  The slope of the tangent line of the curve x^2-xy+y^2=3 at the point (1,2) is equal to 0 (zero, ZERO).


/\/\/\/\/\/\/\/\/

Let me REMIND you that it is commonly accepted among the educated and civilized people to thank for help.

Moreover, expressing gratitude for help is not a "good style" only -- it is MUST.

During weeks, I produce tens first class solutions to visitors, but do not see their expressed gratitude . . .

Do not forget to post your "thanks" to me through the "Thank you" (or "student comments") window.

Otherwise, I will think that I work for idiots . . .