|
Question 1143730: Determine the equation of the circle inscribed in a triangle, if the triangle has its sides on the lines y=0, 4x+3y-50=0, and 3x-4y=0. Sketch the graph.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The lines are
y = 0 (1)
4x + 3y - 50 = 0 (2)
3x - 4y = 0 (3)
 Lines y=0 (red), 4x+3y-50 = 0 (green), 3x-4y = 0 (blue)
The triangle is in QI. Its vertices are
P1 = (0,0) (the intersection points of lines (1) and (3) )
P2 = (12.5,0) (the intersection point of lines (1) and (2) )
P3 = (8,6) (the intersection point of lines (2) and (3) )
Let the point (p,q) be the center of the inscribed circle into the triangle.
Then the point (p,q) is EQUALLY REMOTED from the triangle sides.
So, I will write two equations. One equation will say that the point (p,q) is equally remoted from lines (1) and (2).
Seqond equation will say that the point (p,q) is equally remoted from lines (1) and (3).
The formula for the distance of the point (p,q) on a coordinate plane from the line given by its general equation Ax + By - C = 0 is
d =
Lines y=0 (red), 4x+3y-50 = 0 (green), 3x-4y = 0 (blue)
The triangle is in QI. Its vertices are
P1 = (0,0) (the intersection points of lines (1) and (3) )
P2 = (12.5,0) (the intersection point of lines (1) and (2) )
P3 = (8,6) (the intersection point of lines (2) and (3) )
Let the point (p,q) be the center of the inscribed circle into the triangle.
Then the point (p,q) is EQUALLY REMOTED from the triangle sides.
So, I will write two equations. One equation will say that the point (p,q) is equally remoted from lines (1) and (2).
Seqond equation will say that the point (p,q) is equally remoted from lines (1) and (3).
The formula for the distance of the point (p,q) on a coordinate plane from the line given by its general equation Ax + By - C = 0 is
d = 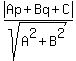 . (4)
So, my first equation is . (4)
So, my first equation is
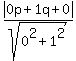 = = 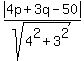 ,
or ,
or
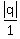 = = 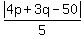 . (5)
The center of the triangle lies, obviously, in QI -- therefore, I can take off the modulus sign in the left part at "q"
(since q is positive in QI (!) )
The center of the triangle lies, obviously, BELOW line (2) -- therefore, 4p+3q-50 < 0 (!). Therefore, I can take off
the modulus sign in the right part, replacing it by the sign " - " (minus).
Then equation (5) takes the form
q = -(4p + 3q -50)/5,
or, in standard equivalent form
4p + 8q = 50. (6)
My second equation is . (5)
The center of the triangle lies, obviously, in QI -- therefore, I can take off the modulus sign in the left part at "q"
(since q is positive in QI (!) )
The center of the triangle lies, obviously, BELOW line (2) -- therefore, 4p+3q-50 < 0 (!). Therefore, I can take off
the modulus sign in the right part, replacing it by the sign " - " (minus).
Then equation (5) takes the form
q = -(4p + 3q -50)/5,
or, in standard equivalent form
4p + 8q = 50. (6)
My second equation is
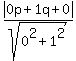 = = 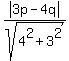 ,
or ,
or
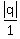 = = 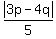 . (7)
Again, similarly to what was said above, I can take off the modulus sign in the left part at "q"
(since q is positive in QI (!) )
The center of the triangle lies, obviously, BELOW line (3) -- therefore, 3p-4q > 0 (!). Therefore, I can take off
the modulus sign in the right part, replacing it by the sign " + " (plus).
Then equation (7) takes the form
q = (3p - 4q)/5,
or, in standard equivalent form
3p - 9q = 0. (8)
Now I have two equations (6) and (8) to find p and q.
4p + 8q = 50, (6)
3p - 9q = 0. (8)
Simplify them
2p + 4q = 25 (6')
p - 3q = 0 (8')
From (8'), express p = 3q and substitute it into (6'). You will get
2*(3q) + 4q = 25,
6q + 4q = 25
10q = 25
q = . (7)
Again, similarly to what was said above, I can take off the modulus sign in the left part at "q"
(since q is positive in QI (!) )
The center of the triangle lies, obviously, BELOW line (3) -- therefore, 3p-4q > 0 (!). Therefore, I can take off
the modulus sign in the right part, replacing it by the sign " + " (plus).
Then equation (7) takes the form
q = (3p - 4q)/5,
or, in standard equivalent form
3p - 9q = 0. (8)
Now I have two equations (6) and (8) to find p and q.
4p + 8q = 50, (6)
3p - 9q = 0. (8)
Simplify them
2p + 4q = 25 (6')
p - 3q = 0 (8')
From (8'), express p = 3q and substitute it into (6'). You will get
2*(3q) + 4q = 25,
6q + 4q = 25
10q = 25
q =  = 2.5.
Then p = 3q = 7.5.
The radius of the circle r is, obviously, equal to q: r = q = 2.5.
Therefore, the equation of the circle is = 2.5.
Then p = 3q = 7.5.
The radius of the circle r is, obviously, equal to q: r = q = 2.5.
Therefore, the equation of the circle is
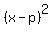 + + 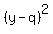 = =  , or , or
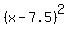 + + 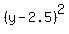 = = 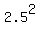 . ANSWER
You can transform it further as you want. . ANSWER
You can transform it further as you want.
The problem is solved.
--------------------
Regarding the basic equation (4), see the lessons
- The distance from a point to a straight line in a coordinate plane
- HOW TO calculate the distance from a point to a straight line in a coordinate plane
- Using formula for the distance from a point to a straight line in a plane to solve word problems
in this site.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is a VERY DIFFERENT solution method, no better and no worse than the one shown by tutor @ikleyn. It shows nicely how two completely different methods can be used to solve a problem, if you have the tools you need.
It should be noted that this method is possible for this example only because the triangle is a right triangle with one side on the x-axis. There are no such restrictions on the general method shown by @ikleyn.
The equations of the lines containing the sides of the triangle are
(1) 
(2) 
(3) 
The slopes of (2) and (3) show that the triangle is a right triangle; and the slope of (3) tells us that the right triangle has side lengths in the ratio 3:4:5.
The x-intercept of line (2) is (12.5,0). That means the hypotenuse of the triangle is 12.5. And that, along with the known 3:4:5 ratio of the side lengths, tells us the lengths of the two legs are 7.5 and 10.
So the perimeter of the triangle is 7.5+10+12.5 = 30; and the area is (1/2)(7.5)(10) = 75/2.
But the area is also one-half the perimeter times the radius of the inscribed circle, so we can find the radius of the circle:



So we have the radius of the circle; now we need to find the center, (h,k).
Since the radius is 5/2 and one side of the triangle is on the line y=0, we know the y coordinate of the center is 5/2. So the center of the circle is (h,5/2).
To find the x coordinate of the center, we can use the fact that the measure of the angle between the x-axis and the line from the origin to the center of the circle is half the measure of the angle of the triangle at the origin.


So


We now have the radius of the circle and the coordinates of the center of the circle, so we can write the equation of the circle:
center(15/2,5/2), radius 5

|
|
|
| |