SOLUTION: 5 men can prepare 10 toys in 6 days working 6 hours a day. In how many days can 12 men prepare 16 toys working 8 hours a day?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: 5 men can prepare 10 toys in 6 days working 6 hours a day. In how many days can 12 men prepare 16 toys working 8 hours a day?       Log On


   

Question 1143725: 5 men can prepare 10 toys in 6 days working 6 hours a day. In how many days can 12 men prepare 16 toys working 8 hours a day?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
-----------------------------------------------------------------
5 men can prepare 10 toys in 6 days working 6 hours a day.
-----------------------------------------------------------------

Six days at six hours per day makes 36 HOURS.
5r%2A36=10
r=10%2F%285%2A36%29
r=1%2F18


--------------------------------------------------------------------
In how many days can 12 men prepare 16 toys working 8 hours a day?
--------------------------------------------------------------

x, number of HOURS
12%281%2F18%29x=16
%282%2F3%29x=16
x=%283%2F2%2916
x=24%7D%7B%7B%7Bhours

Working at 8 hours per day, this is 3 days.

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

One way to solve it : 

Making 10 toys requires  5 men * 6 days * 6 hours = 180 men-hours, according to the first statement.


Hence, making 1 toy requires 180/10 = 18 hours.


Then making 16 toys will take 16*18 = 288 hours.


12 men, working 8 hours per day, will do it in 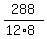 288%2F%2812%2A8%29 = 3 days.


Answer.  In 3 days.


Another way to solve the problem is THIS : 

Based on the first statement, rate of work of 1 man is 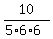 10%2F%285%2A6%2A6%29 = 10%2F180 = 1%2F18 of the toy per hour.


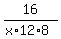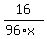If "x" is the number of days under the question, then the rate of work of one man is  16%2F%28x%2A12%2A8%29 = 16%2F%2896%2Ax%29 of the toy per hour.


Rate of work is assumed to be the same in both cases; it gives you an equality  (proportion)


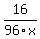     1%2F18 = 16%2F96x.


From the proportion


     1*96x = 18*16,   or   x = 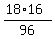%2818%2A16%29%2F96 = 3.


You get the same answer :  3 days are needed.

You can use either of the two ways/methods to solve the problem.

---------------

See the lesson
    - Rate of work problems
in this site,  where you can find many other similar solved problems.