Question 1143612: The length of a rectangle is 14 m longer than its width and the area of the rectangle is 400 m2. Find the exact dimensions of the rectangle.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!


That's not going to factor to give rational numbers.
Use the quadratic formula to get an exact answer in radical form, or a graphing calculator to get a decimal approximation.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let y be the value exactly half-way between the length and the width.
Then the length = y+7. while the width = y-7.
The area is the product of length and width, i.e. (y+7)*(y-7) = 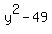 .
Then the area equation is .
Then the area equation is
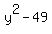 = 400,
which implies = 400,
which implies
 = 400 + 49 = 449,
y = = 400 + 49 = 449,
y = 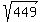 .
Thus the length = .
Thus the length = 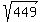 + 7 = 28.190 (approximately, with 3 right decimal places). ANSWER
and the width = + 7 = 28.190 (approximately, with 3 right decimal places). ANSWER
and the width = 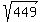 - 7 = 14.190 (approximately, with 3 right decimal places). ANSWER
CHECK. The product of - 7 = 14.190 (approximately, with 3 right decimal places). ANSWER
CHECK. The product of 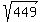 + 7 and + 7 and 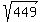 - 7 is 400 = 449-49, and the difference is 14, obviously. - 7 is 400 = 449-49, and the difference is 14, obviously.
Solved.
---------------------
Surely, this method is the same as to solve the problem using the quadratic formula, and it gives the same answer.
Its advantage is in that it is not so boring . . .
/\/\/\/\/\/\/
To see many other problems solved by the similar method, look into the lessons
- HOW TO solve the problem on quadratic equation mentally and avoid boring calculations
- Three methods to find the dimensions of a rectangle when its perimeter and the area are given
- Three methods to find the dimensions of a rectangle when its area and the difference of two dimensions are given
in this site.
|
|
|