Question 1143539: Suppose that two dice are tossed. For each die, it is equally likely that 1, 2, 3, 4, 5, or 6 dots will turn up. Let S be the sum of the two dice.
a. Let E1 be the event that the first die shows a 3. Let E2 be the event that S is 6. Are E1 and E2 independent events?
b. Given that the first die shows a 3, what is the probability that S is an even number?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) We should check if P (E1 & E2) = P(E1)*P(E2).
Calculation P(E1) is easy: P(E1) =  , since there are 6 outcomes for the first die,
showing the numbers 1, 2, 3, 4, 5 and 6 with equal probabilities.
To calculate P(E2), notice that the sum of 6 of two dice can be obtained in 5 (five) cases
(1,5), (2,4), (3,3), (4,2) and (5,1),
So the event E2 has the probability P(E2) = , since there are 6 outcomes for the first die,
showing the numbers 1, 2, 3, 4, 5 and 6 with equal probabilities.
To calculate P(E2), notice that the sum of 6 of two dice can be obtained in 5 (five) cases
(1,5), (2,4), (3,3), (4,2) and (5,1),
So the event E2 has the probability P(E2) = 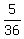 .
Now, the event (E1 & E2) is the intersection of E1 and E2;
in other words, first die shows a "3", while the sum of the faces of the two dice is 6.
It may happen if and only if BOTH dice face up a "3" -- the event with the probability .
Now, the event (E1 & E2) is the intersection of E1 and E2;
in other words, first die shows a "3", while the sum of the faces of the two dice is 6.
It may happen if and only if BOTH dice face up a "3" -- the event with the probability  , obviously.
Thus we have P(E1) = , obviously.
Thus we have P(E1) =  ; P(E2) = ; P(E2) = 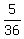 and P(E1 & E2) = and P(E1 & E2) =  .
The product of probabilities P(E1)*P(E2) = .
The product of probabilities P(E1)*P(E2) =  } = } = 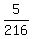 is not equal to P(E1 & E2) = is not equal to P(E1 & E2) =  --
hence, the two events E1 and E2 ARE NOT INDEPENDENT. ANSWER
(b) If the first die faces up a "3", then the sum is even in these 3 (three) cases
(3,1), (3,3), (3,5).
So the probability for S to be an even number is --
hence, the two events E1 and E2 ARE NOT INDEPENDENT. ANSWER
(b) If the first die faces up a "3", then the sum is even in these 3 (three) cases
(3,1), (3,3), (3,5).
So the probability for S to be an even number is 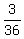 = =  . ANSWER . ANSWER
--------------
If you want to learn this subject wider and deeper, look into my lesson
- Rolling a pair of fair dice
in this site.
|
|
|