Question 1143477: Donald has a pair of blue shoes, a pair of red shoes, and a pair of white shoes. He
wants to put these six shoes side by side in a row. However, Donald wants the left
shoe of each pair to be somewhere to the left of the corresponding right shoe. How
many ways are there to do this?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's the same as the number of distinguishable arrangement of the row of 6
letters BBRRWW.
That's because For any distinguishable arrangement of those 6 letters, we
can always put the left shoe of each color left of the right one of the same
color.
Since there are 6 letters, the 2 B's are indistinguishable, the 2 R's are
indistinguishable and the 2 W's are indistinguishable.
So the answer is  Edwin
Edwin
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
My answer is the same as Edwin's answer: 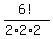 = = 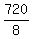 = 90, = 90,
but my logic (and wording presentation) is different.
The total number of permutations of 6 items is 6! = 720.
In this set of all permutations, S(6), exactly HALF of all permutations has the "leftBLUE" item on the left from "rightBLUE" item.
So, regarding blue shoes, we have the subset in S(6) of 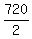 permutations,
where red shoes are in the right order.
Let denote this subset as S(6,B).
In the subset S(6,B), exactly HALF of its permutations has the "leftRED" item on the left from "rightRED" item.
So, regarding red AND blue shoes, we have the subset in S(6,R) of permutations,
where red shoes are in the right order.
Let denote this subset as S(6,B).
In the subset S(6,B), exactly HALF of its permutations has the "leftRED" item on the left from "rightRED" item.
So, regarding red AND blue shoes, we have the subset in S(6,R) of 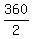 = 180 permutations,
where BOTH red AND blue shoes are in the right order.
Let denote this subset as S(6,B,R).
In the subset S(6,R,B), exactly HALF of its permutations has the "leftWHITE" item on the left from "rightWHITE" item.
So, regarding red, blue and white shoes, we have the subset in S(6,R,B) of = 180 permutations,
where BOTH red AND blue shoes are in the right order.
Let denote this subset as S(6,B,R).
In the subset S(6,R,B), exactly HALF of its permutations has the "leftWHITE" item on the left from "rightWHITE" item.
So, regarding red, blue and white shoes, we have the subset in S(6,R,B) of  = 90 permutations,
where all red AND blue AND white shoes are in the right order.
It gives the final answer. = 90 permutations,
where all red AND blue AND white shoes are in the right order.
It gives the final answer.
Solved.
|
|
|