Question 1143426: The graph of cos(T) is shifted left 270°, has the period decreased to 180°, and is shifted up 2 units. What is the transformed equation?
Found 2 solutions by KMST, greenestamps:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The graph of  (with (with  in degrees) has a period of in degrees) has a period of  . .
In every period there is a single maximum value of  , such as at , such as at  . .
 goes through a maximum at goes through a maximum at  , and as , and as  increases, increases,
it has the next maximum at  . .
After that, the next maximum is at  , and so on. , and so on.
Here is a piece of the graph of  with with  in degrees: in degrees:
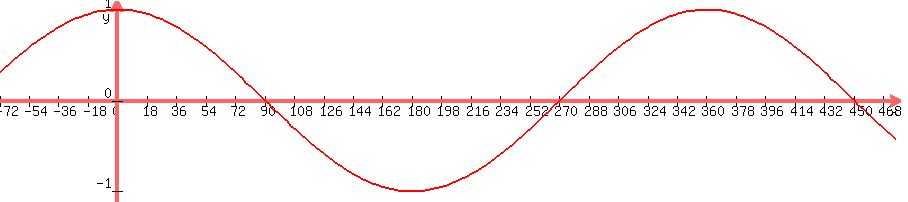 , ,
We want to do 3 changes to get to the "transformed equation", and there often is more than one way to get to a destination, but some ways may be "smoother sailing" compared to others.
CHANGES IN THE ORDER LISTED:
If we want shift the graph 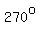 to the left, we would end with a maximum at to the left, we would end with a maximum at 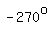 . .
A way textbooks suggest to do that shift is replacing the variable with another, such as replacing  . .
hat way the point for  is at is at  . .
We would have  . .
The graph of  as a function of as a function of  is shown below. is shown below.
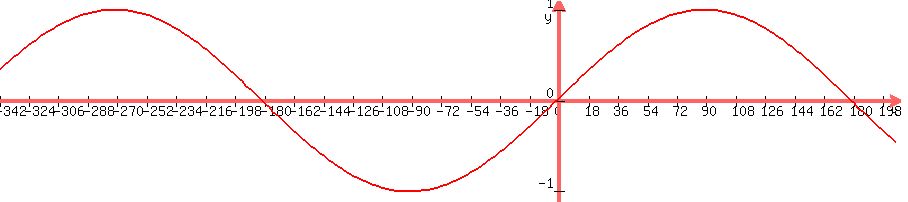
If after that we want to change the period to  , ,
we can do that by changing to variable  , so that it increases twice as fast as , so that it increases twice as fast as  . .
If we still want the maximum at 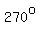 , we need to make , we need to make  , ,
and change the function from  to to  . The graph of . The graph of  as a function of as a function of  is shown below. is shown below.
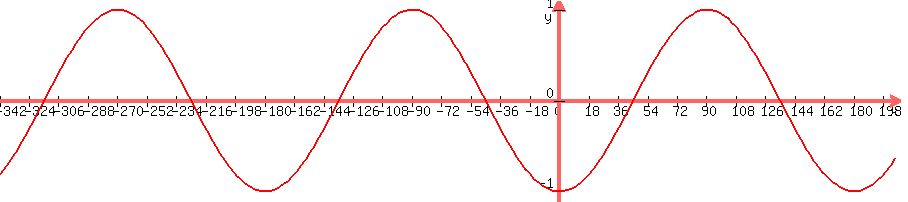
Finally, to shift an x-y graph up by two units, we just add  to the expression for to the expression for  . .
The graph of  as a function of as a function of  is shown below. is shown below.

A DIFFERENT WAY:
With  , we change the function from , we change the function from  to to  , ,
and that changes the period from  to to  . .
The graph of  as a function of as a function of  is shown below. is shown below.

To shift the graph 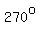 to the left we change to the left we change  to to 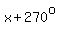 to get to get 
Finally, we add  to shift the graph up by to shift the graph up by  units, and get units, and get  . .
NOTE: There are other expressions with the same graph, such as  : :
 . .
Answer by greenestamps(13209)   (Show Source): (Show Source):
|
|
|